01) Um Corpo rígido de massa é formado por duas barras, e , soldadas perpendicularmente em (ponto médio de ), conforme ilustrado na figura. Estas barras são homogêneas, esbeltas e tem comprimento cada. A extremidade do corpo rígido encontra-se articulada a um bloco que desliza sobre uma guia horizontal com uma aceleração , conhecida. Pede-se:
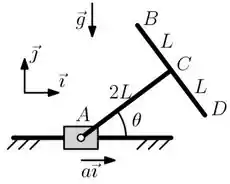
a) O vetor posição do centro de massa do corpo rígido formado pelas barras e .
b) O momento de inércia , do corpo rígido com respeito ao eixo .
c) O diagrama de corpo livre do corpo rígido.
d) O valor do ângulo para o qual a aceleração angular do corpo rígido é nula.
Dado: o momento de inércia de uma barra homogênea e esbelta de massa e comprimento com respeito a um eixo perpendicular passante por seu centro de massa é igual a .
Passo 1
Faaala gente bonita, como vocês estão?
Nessa questão temos um corpo rígido meio diferente, imagina pegar duas barras e juntá-las formando um T, pronto, esse é o corpo ABCD. Essa estrutura encontra-se articulada em , um bloco que desliza horizontalmente, com aceleração
a) Aqui devemos encontrar o vetor , que liga e o centro de massa do corpo rígido.
Beleza, mas como podemos calcular o centro de massa desse corpo tão diferente?

Então, a ideia é primeiro calcular o centro de massa de cada uma das barras, e depois realizar uma média ponderada usando os vetores de cada um dos CM’s em relação a , pra já sair com a resposta.
Começando pela barra , como ela é homogênea, temos um centro de massa bem no seu meio. Logo:
Analogamente, para a barra , o seu centro de massa está no seu centro (o ponto ). Assim:
Juntando as duas, para descobrir o vetor , podemos usar a seguinte média ponderada:
Top!
No enunciado também é falado que a massa total do corpo rígido, é dada por:
Com as barras são idênticas, temos:
Substituindo na nossa média ponderada, vem:
Logo:
Bouaaa! De uma vez só já encontramos esse vetor.
Vamo pra próxima!
Passo 2
b) Agora devemos determinar o momento de inércia em relação ao eixo .
Como foi dado no enunciado, o momento de inércia de uma barra homogênea, esbelta, de comprimento , toda perfeitinha, em relação a um eixo que passa pelo seu centro geométrico vale:
Beleza... o problema é que nosso corpo rígido não é uma barra esbelta, ele tem a forma de T. E aí, o que dá pra fazer nesse caso?

Calma Buzz, tem uma ideia legal! Podemos considerar o corpo rígido com a junção das barras e e daí considerar:
Top! Vamo começar pela barra .
Pelo dado da questão, sabemos que:
Só que isso é em relação a pra descobrir em relação a podemos usar o teorema dos eixos paralelos. Daí, por ele, vem:
Seguindo o mesmo raciocínio para a barra , temos:
Aplicando o teorema dos eixos paralelos, vem:
Excelente! Somando o momento de inércia das duas barras, vamos ter:
Bouaaa! Conseguiram entender bem essa ideia? Anota ela aí que essa foi ótima 😊
Passo 3
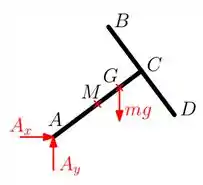
c) Devemos desenhar o diagrama de corpo livre do corpo rígido.
Pra desenhar o DCL é bizu sempre começar identificando as forças que agem no corpo.
Assim, em , temos a força peso do conjunto agindo em , como também as reações horizontal e vertical no apoio em .
E é só isso mesmo, desenhando temos:
Passo 4
d) Finalmenteee, chegamos à última parte da questão.
Pra finalizar, precisamos determinar o valor de para que o corpo rígido tenha aceleração angular nula.

O negócio é pensar com calma, a gente quer usar a informação de que pra determinar o valor de . Então bora partir pro TQMA, com polo em . Como , temos:
Só que, pelo próprio DCL do corpo rígido, podemos perceber que:
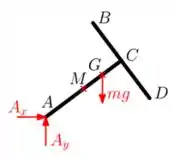
Assim, igualando as duas expressões e lembrando também que vem:
Daí:
Portanto:
Aeeee, Prontinho! Mais uma questão encerrada.
Vamo continuar no gás galera!! Força hahaha
Resposta
a)
b)
c) Resolução no texto.
d)