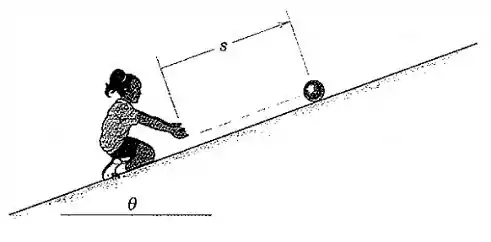
Uma menina rola uma bola para cima em um plano inclinado e deixa esta retornar para ela. Para o ângulo e a bola em questão, a aceleração da bola ao longo da inclinação é constante em , dirigida para baixo no plano inclinado. Se a bola é liberada com uma velocidade de , determine a distância em que esta se move para cima no plano inclinado antes de inverter o seu sentido e o tempo total necessário para a bola retornar à mão da criança.

Nesse exercício a aceleração é constante, então podemos usar uma equação daquele conjunto que temos para aceleração constante. Repare que temos a velocidade inicial e ele quer saber no primeiro item a distância percorrida.

Vamos usar uma equação que tenha essas variáveis:

Vamos ver o que temos de dados do exercício. Temos a velocidade inicial que é , temos também a aceleração que é , onde esse sinal de menos é porque foi dito que a aceleração é dirigida para baixo no plano inclinado e a bolinha está subindo o plano. Com essa mesma informação, vemos que não é necessário decompor a aceleração, pois ela está ao longo do plano.

Consideramos a gravidade como . Agora vamos analisar as informações a mais que ele nos deu: ele disse que quer saber a distância em que a bola se move para cima no plano inclinado antes de inverter o seu sentido. O que isto quer dizer?

Quando a bola inverte seu sentido, ou seja, quando ela começar a descer o plano, ela precisa ter a velocidade igual a zero. Então, no momento de transição temos que .

Falta agora sabermos qual a posição inicial da bola. Mas repare que a bola é lançada a partir de um ponto e retorna para este mesmo ponto. Ou seja, podemos arbitrar que a posição inicial começa no zero:

Pronto, agora podemos calcular a posição final da bolinha: