01) Uma polia de centro , raio e peso , é vinculada à extremidade da barra . Um bloco de peso mantém-se em equilíbrio suspenso por um fio ideal apoiado sobre a polia e ligado à barra , conforme indicado na figura. As barras e , ambas de peso desprezível, são ligadas entre si através da articulação . A extremidade da barra apoia-se em uma parede vertical rugosa, ao passo que a extremidade da barra é vinculada a essa parede por meio da articulação . Pede-se:
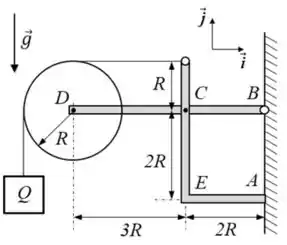
a) desenhar os diagramas de corpo livre da polia e das barras e
b) determinar os esforços reativos em e em ;
c) determinar o valor mínimo do coeficiente de atrito para que o conjunto se mantenha em equilíbrio estático.
Passo 1
Faaala galerinha, como vocês estão?
a) Nessa questão temos uma estrutura em equilíbrio estático. Ela é composta por uma polia e duas barras, e , que estão articuladas entre si no ponto . A barra apoia-se numa parede rugosa, já está articulada na parede no ponto .
Nesse primeiro item devemos desenhar o diagrama de corpo livre (DCL) da polia e das barras.
Sempre que queremos fazer DCL’s é importante identificar primeiro as forças que estão agindo em cada elemento.

Começando pela barra , ela está articulada em três pontos. Cada um desses fornecerá uma reação no eixo , e outra no eixo . Daí, é só supor algum sentido inicial, temos:
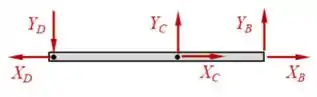
Show! Já na barra temos apenas ponto de articulação (ponto ), onde também teremos duas reações, uma em e outra em .
Além disso, também é falado que essa barra está apoiada na parede rugosa. Assim, por estar apoiada na parede, ela recebe uma normal no sentido , e pela parede ser rugosa, há uma força de atrito apontando para .
Por fim, o fio preso ao peso também está preso na extremidade de .
Logo:
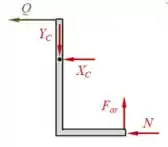
Uma observação importante é que, como o nó está em equilíbrio (resultante nula), já desenhamos as reações que essa articulação faz na barra como sendo o oposto da reação que a mesma articulação faz em .
Por último, temos a nossa querida polia.
Basicamente, temos a articulação em , que também provoca uma reação em e outra em .
Temos também a reação à força que o fio faz na polia, tanto na direção vertical como horizontal. Daí, podemos desenhar:
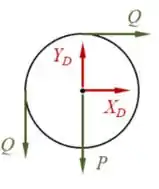
Só precisamos tomar cuidado com o sentido de , pois eles devem ser opostos no DCL da polia e da barra, já que se trata de um par ação e reação 😊
Passo 2
b) Agora nosso objetivo é determinar os esforços reativos, ou seja, e agindo em , como também e que atuam em .
Pô, e como que a gente faz pra relacionar todas essas variáveis em equações?

Isso! É só usar a lei de Newton, ou o teorema da resultante, para cada um dos elementos. Lembrando que tudo está em equilíbrio, logo .
Começando pela Polia:
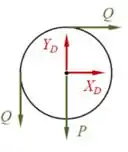
Logo:
Massa! Bora analisar a barra :
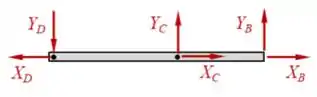
Substituindo as equações da polia, vem:
Escrevendo a equação do momento em relação a temos também:
Daí:
Só que:
Assim:
Boa! Já descobrimos algumas variáveis.
Passo 3
Por último, pra calcular as variáveis que faltam, vamos escrever as equações do equilíbrio para a barra :
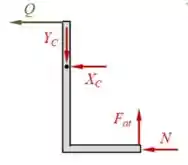
Daí, já temos que:
Aplicando o momento em relação a , também podemos escrever:
Isolando a normal , vem:
Excelente! Substituindo esse resultado na equação escalar do equilíbrio em da barra , ficamos com:
Como pra matar esse item só falta descobrir o valor de , bora substituir esse resultado na equação em , da barra . Logo:
Prontinho! Matamos mais um item.
Passo 4
c) Pra finalizar o último item dessa questão, devemos calcular o valor mínimo do coeficiente de atrito entre a barra e a parede, de modo que o conjunto permaneça em equilíbrio.
Mas eaí, vocês lembram da fórmula da força de atrito?

Hahaha, pegadinha galera! Isso é algo que muita gente confunde, mas na real que a força de atrito não tem fórmula mesmo. O que ela tem é apenas uma desigualdade que determina o seu valor máximo:
Assim, substituindo os valores que já calculamos anteriormente, temos:
Logo, o valor mínimo do coeficiente de atrito acontece exatamente na igualdade:
Ufaaa!! Terminamos mais uma questão 😊
Espero que vocês tenham entendido bem direitinho, até a próxima galera!!
Resposta
a) Resolução no texto
b)
c)