A velocidade de um automóvel, inicialmente em repouso em , varia de acordo com , onde é dado em segundos. Determine os módulos da velocidade e da aceleração do carro quando .
Passo 1
O enunciado nos deu a aceleração do carro como uma função do tempo:
Então, no tempo vamos ter o seguinte valor para aceleração:
E a velocidade? Se precisamos derivar a velocidade com relação ao tempo para achar a aceleração... Se o que temos é a aceleração, como fazemos para achar a velocidade? É isso aí, temos que integrar:
Considerando :
Então, no tempo :
Passo 2
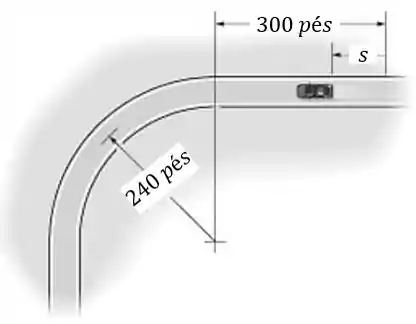
Agora, repare pelo desenho que o carro anda em um trecho retilíneo e depois começa a fazer uma trajetória circular. Temos que analisar se em o carro está na parte reta ou já entrou na curva. Para isso, vamos achar a posição final do carro.
Sabemos que a velocidade é a derivada do deslocamento com relação ao tempo. Então, se temos a equação da velocidade em função do tempo, como iremos calcular o deslocamento? É só integrar a equação da velocidade:
O enunciado nos disse que o carro parte do repouso e, então:
Então, no tempo vamos ter que:
Ou seja, o carro percorreu toda a parte reta e entrou na curva!
Passo 3
A velocidade final no tempo não muda independentemente do movimento se dar numa reta ou numa curva. Mas.... A aceleração não será a mesma. Lembra que o movimento retilíneo pode possuir duas componentes: a aceleração centrípeta e a aceleração tangencial.
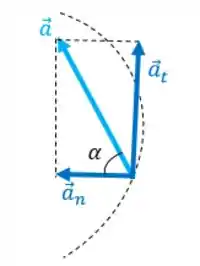
E por que eu disse pode possuir? Porque a componente tangencial só existe quando há variação de velocidade. O que ocorre no nosso caso, pois o carro começa com uma velocidade inicial zero e desenvolve uma velocidade que varia em função do tempo.
Então, vamos calcular cada componente da aceleração e depois achar a resultante.
No movimento curvilíneo a aceleração tangencial é calculada usando a equação que foi dado no enunciado para:
A aceleração centrípeta é calculada usando a seguinte fórmula:
Onde, é o raio da curvatura. No nosso caso .
A velocidade nós vimos que não muda, então . Portanto, a aceleração centrípeta será:
Vamos calcular o módulo da aceleração agora: