Encontre a intensidade do campo magnético no centro da espira devido a corrente que circula pela mesma, conforme a figura abaixo:
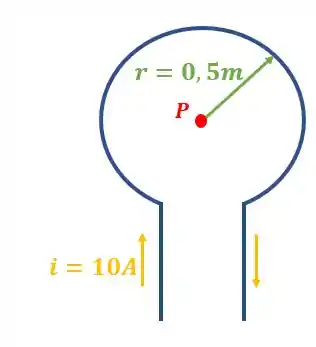
Passo 1
Primeiro, devemos lembrar que o cálculo do módulo do campo magnético em uma espira circular é igual a:
Então o campo magnético varia de acordo com a corrente elétrica que percorre a espira de raio , além da permeabilidade magnética do vácuo .
Passo 2
Os valores que nos foram dados são:
E a permeabilidade magnética do vácuo é igual a:
Passo 3
Então substituindo esses valores na equação:
Temos:
Multiplicando os números do numerados:
A multiplicação entre duas potências de , como se trata da mesma base e expoentes diferentes, nós mantemos a base e somamos os expoentes:
Logo:
A multiplicação no denominador da fração:
Então:
Qualquer divisão por é igual ao próprio número, então o módulo do campo magnético é igual a :
Passo 4
Quando um número está multiplicado por , nós podemos substituir pelo prefixo micro que acompanhará a unidade, então: