Seja um cubo isolante e uniformemente carregado, isolado de todos os outros corpos.
Dentre as afirmações:
- A lei de Gauss só se aplica a esse problema se escolhermos superfícies gaussianas cúbicas, haja vista a simetria do sistema.
- A lei de Gauss deixa de ser aplicável a esse problema se escolhermos superfícies gaussianas que interceptam o cubo carregado.
- A lei de Gauss simplesmente não se aplica a esse problema.
Qual(is) é(são) verdadeira(s)?
- Somente a I
- Somente a II
- Somente a III
- Somente a I e a II
- Somente a I e a III
- Somente II e a III
- Todas estão corretas.
- Nenhuma está correta.
Passo 1
Vamos analisar juntos todas as alternativas, começando pela primeira:
A lei de Gauss só se aplica a esse problema se escolhermos superfícies gaussianas cúbicas, haja vista a simetria do sistema.
Bom pessoal, a Lei de Gauss só especifica que a superfície gaussiana deve ser fechada em torno da carga que desejamos calcular o fluxo, mas não fala de sua forma.
Então a superfície pode ter qualquer formato, como esfera, cilindro, cubo ou até mesmo uma bem estranha, desde que englobe todas as cargas.
Por exemplo:
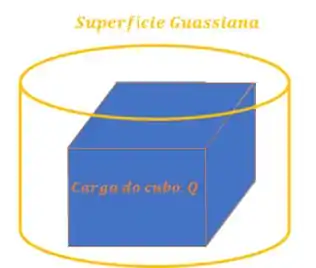
A afirmativa é falsa!
Passo 2
A segunda afirmativa diz:
A lei de Gauss deixa de ser aplicável a esse problema se escolhermos superfícies gaussianas que interceptam o cubo carregado.
A Lei de Gauss continua se aplicando se cortar o cubo, a única coisa que vai mudar é que teremos apenas parte da carga do cubo no interior da superfície gaussiana, veja:
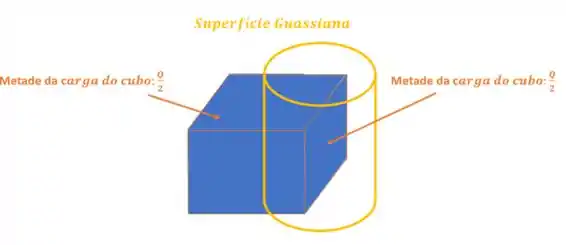
Então a afirmativa é falsa!
Passo 3
A última afirmativa é:
A lei de Gauss simplesmente não se aplica a esse problema
Já vimos que a Lei de Gauss se aplica a esse problema. O único desafio é escolher a melhor superfície gaussiana que facilite os cálculos.
Então a afirmativa está incorreta!
Logo nenhuma das afirmativas está correta e a resposta certa será a letra “h”!
Resposta
h) Nenhuma está correta.