Uma construtora quer colocar uma ponte ligando os pontos e em lados diferentes de um rio. Os operários, estando em , precisam calcular a distância entre esses pontos. Dispunham apenas de um teodolito. Do ponto A. foram até o ponto , na mesma margem a quilômetros de distância. Os ângulos que obtiveram são e . Determine a distância entre e .
Passo 1
Bem, a primeira coisa a fazer é esboçar o problema. É formado um triângulo na seguinte forma:
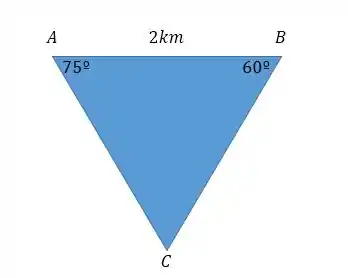
Sendo que é o ângulo no vértice formado pelos lados compostos por e e é o ângulo no vértice formado pelos lados compostos por e .
Passo 2
Chamando o ângulo em de , Pela lei dos senos, temos que:
E queremos achar que é justamente a distância entre os pontos e . Não sabemos e , mas, como a soma dos ângulos de um triângulo é , concluímos que:
E:
Portanto:
Finalmente: