Na figura abaixo , , e . Qual a medida de ?
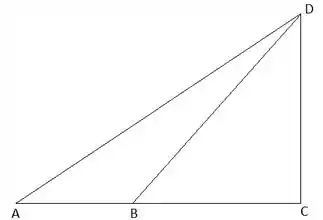
Passo 1
Nessa nem precisamos esquematizar o problema, já o temos em mão. Vamos ignorar as unidades por enquanto e visualizar o que importa:
Marcando isso tudo na figura: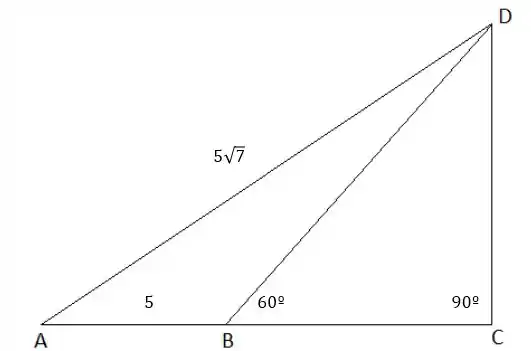
Passo 2
A partir desses valores, podemos encontrar os outros. Veja que:
Logo:
Com esse ângulo, podemos usar a lei dos cossenos para achar :
Pelo círculo trigonométrico, tiramos que:
Assim:
Tendo raízes:
Mas a única que vale é a positiva, pois é uma medida.
Passo 3
Queremos chegar em , mas veja que o triângulo é retângulo, então podemos usar as relações trigonométricas sem medo. Considerando o ângulo de referência, é o cateto oposto e é a hipotenusa. Assim sendo, podemos usar o seno:
Relembrando a unidade: