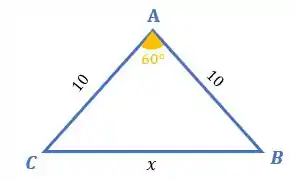
O valor da medida do lado do triângulo abaixo vale:
- 10
- 20
- 30
- 40
- 50
Passo 1
Falaaaaa Aíí!! Vamos ver como podemos encontrar o valor de no triângulo do enunciado??

Primeira coisa que podemos reparar é que o triângulo não é retângulo. É um triângulo qualquer. Beleza... Então, se você reparar, nós temos o valor de lados do triângulo e estamos trabalhando com o valor de um ângulo oposto a um desses lados, concorda? Nesse caso, faz sentido pra gente utilizar a lei dos cossenos para resolver esse exercício!
Passo 2
A lei dos cossenos nos diz o seguinte
Onde e são os lados do trângulo e o ângulo. Assim, substituindo os valores do triângulo, temos
Beleza?! Mas... e agora??
Agora precisamos lembrar o valor de . Para isso, basta olharmos para a tabelinha de ângulos notáveis:
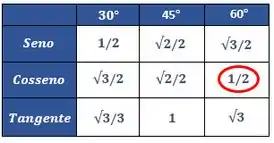
Assim, substituindo o valor na equação, temos
Fazendo as continhas, temos
Ou seja,
Portanto,
Show de bola?!