Três ilhas , e aparecem num mapa em escala , como na figura. Das alternativas, a que melhor se aproxima de distância entre as ilhas e é:
Passo 1
Vamos lááááá!!! Geralmente, o melhor caminho para resolver exercícios que apresentam dois ângulos e um lado de um triângulo é a lei dos senos

A lei dos senos nos diz o seguinte
Onde e são os ângulos do trângulo e e os lados. Algo importante é que é o lado oposto ao ângulo . Da mesma forma, é o lado oposto ao ângulo .
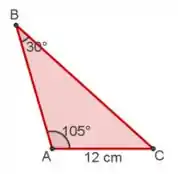
Beleza?! Então vamos olhar para o nosso triângulo. Observe que o segmento é oposto ao ângulo . Pela soma das medidas internas de um triângulo, podemos concluir que o ângulo mede , show de bola?!

Os lados que serão usados nesse problema são e . Os ângulos opostos a esses lados são: e , respectivamente. Substituindo esses valores na lei dos senos, temos
Passo 2
Multiplicando cruzado, temos
Vamos agora olhar para a tabelinha dos ângulos notáveis para encontrar os valores dos acima
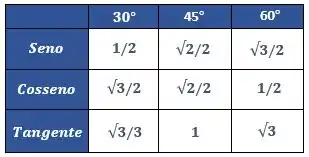
Assim, temos
Fazendo as continhas,
Terminamos??? Se você reparar não temos essa opção nas alternativas. Então, vamos substituir o valor da .
Portanto,
Passo 3
Terminamos??? NÃÃÃO!

O valor de que encontramos está em centímetros! Precisamos converter para Quilômetros! Assim,
Portanto, nossa resposta é a letra E!!