Dois lados de um triângulo medem e e formam um ângulo de . O terceiro lado desse triângulo mede:
Passo 1
Vamos lááááá!!! Geralmente, o melhor caminho para resolver exercícios que apresentam dois lados e um ângulo entre eles de um triângulo é a lei dos cossenos.

Beleza... Então, o lado oposto ao ângulo será e todos esses lados serão colocados na fórmula seguinte
Ahh, e são os lados que formam o ângulo.
Passo 2
Substituindo os valores na fórmula, temos
Fazendo as continhas,
Beleza?! Mas... e agora??
Agora precisamos lembrar o valor de . Para isso, basta olharmos para a tabelinha de ângulos notáveis:
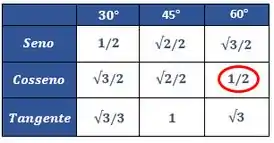
Assim, substituindo o valor na equação, temos
Fazendo as continhas, temos
Ou seja,
Portanto,
Show de bola?!
