(Cap 22 Ex – 48) Na figura abaixo, um elétron (e) é liberado a partir do repouso no eixo central de um disco uniformemente carregado de raio R. A densidade superficial de cargas do disco é. Determine o módulo da aceleração inicial do elétron se for liberado a uma distância (a) R, (b) R/100, (c) R/1000 do centro do disco. (d) Por que o módulo da aceleração quase não varia quando o elétron está próximo do disco?
Passo 1
Falaiii galerinha do responde ai, de boa na lagoa?
Bora resolver essa comigo?
Encostaaaa!!
Letras (a), (b) e (c)
Vamos fazer os três primeiros itens de uma vez. Pensa comigo: se a gente souber o campo elétrico que o disco produz lá onde está o elétron, você concorda comigo que a gente consegue calcular a aceleração?
É só usar aquela velha equação:
Como nós já sabemos quanto vale “e” (carga elementar) e “” (massa do elétron), pois são valores tabelados, a gente “só” precisa achar o campo E.
Aí que mora o problema. Mas não temos medo de problemas, temos?
A gente não sabe achar (ainda) o campo gerado por um disco como aquele da figura do enunciado, mas nós sabemos o campo gerado por um pequeno anel.
Quando a gente diz pequeno anel, na prática, é um anel com espessura muito pequena, tipo uma circunferência. Olha a figura, o anel é aquele amarelinho:
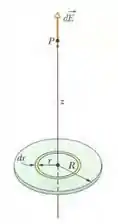
A estratégia, meu povo, é pegar a contribuição de todos os anéis e somar tudo. Contribuição de várias coisas pequenas lembra o quê? Isso mesmo, vamos integrar.
Passo 2
Vamos precisar da equação do campo que o pequeno anel gera em um ponto P distante z acima do centro do anel:
Onde q é a carga do anel e K é o K de sempre, a constante eletrostática.
Eu sei que é meio chato jogar a fórmula, mas é por causa do seguinte: achar o campo elétrico que um anel gera, é, por si só, uma questão, e que está resolvida na página 29 do Halliday da nona edição 😉.
Sim, para resolver essa questão, precisaríamos resolver duas questões, na verdade.
O próximo passo é trocar “E” por ”dE” e ”q” por ”dq”, porque vamos pegar não um, mas vários anéis com raios diferentes. Cada anelzinho de raio “r” produz um campo:
Vamos integrar!
Será que a gente cosegue integrar o lado direito? Da forma que está, não dá. A variável do integrando é o “r” e a diferencial é “dq”.
Mas se em vez de “dq” fosse ”dr” a gente conseguiria?
Aí, sim, a gente consegue.
Então vamos fazer isso.
Pra isso, vamos usar a densidade superficial de carga (que vamos chamar de ), até por isso que o enunciado deu.
Vamos lá: o que é a densidade superficial de carga?
Não é carga dividido pela área? Então:
Agora deriva implícito dos dois lados (aquele negócio de derivar e escrever a diferencial do lado)
Entre parêntesis coloquei as derivadas. Então fica assim:
Passo 3
Agora pega isso e joga lá naquela integral:
Essa integral a gente resolve assim oh: chama . Então (apenas derivei implícito e cortei o dois que aparece). Agora pega essas duas coisas e substitui lá na integral.
Como
temos
Então, fica assim oh
Substituindo os limites de integração dá isso aqui:
Ufa! Achamos o campo gerado pelo disco. Agora estamos quase no fim.
Passo 4
Só precisamos agora usar aquela equação:
Para resolver os itens (a), (b) e (c), vamos trocar z por R, R/100 e R/1000, respectivamente:
(a):
(b):
(c):
Passo 5
Letra (d)
Uma forma (correta) de explicar é o fato de que quando o elétron está bem perto do centro, ele não “sente” os efeitos das bordas.
A outra maneira, que eu prefiro, é pensar que o disco se comporta como uma placa infinita quando o elétron está muito próximo. E daí?
Daí que uma placa infinita tem campo elétrico constante, então produz uma aceleração constante.
Se essa história de aproximar o disco por uma placa infinita não te convence, devo te dizer que você faz isso o tempo inteiro.
Você diz que perto da terra a gente acelera pra baixo com aceleração constante g, mas se você estudou gravitação sabe que a aceleração muda com a distância até o centro da Terra.
Você sabe disso, mas diz que é sempre g mesmo e não tá nem aí, porque perto da superfície terrestre quase não faz diferença a altura, mesmo.
O g muda muuuito pouco. Com o elétron e o disco é EXATAMENTE a mesma coisa.
Resposta
Letra (a):
Letra (b):
Letra (c):
Letra (d): Perto do centro, o elétron não sente os efeitos das bordas.