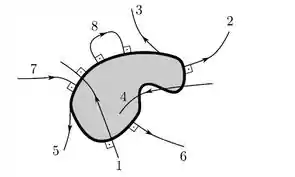
Na figura, temos uma seção tranversal de um corpo condutor, isolado (muito afastado de quaisquer outros corpos), em equilíbrio eletrostático, carregado positivamente, além de algumas curvas orientadas. Qual(is) de tais curvas, nitidamente, não pode(m) representar linhas de campo do correspondente campo eletrostático?
(a) 1 e 4.
(b) 1, 4 e 8.
(c) 2, 6 e 7.
(d) 1, 3, 4, 5, 7 e 8.
(e) 1, 3, 4, 5 e 8.
Passo 1
Esse exercício se torna muito simples se aplicarmos apenas 4 regras. São elas:
1) Linhas de campo saem de objetos carregados positivamente e entram em objetos carregados negativamente.
2) Não pode haver linhas de campo dentro de um material condutor em equilíbrio eletrostático. Pois, se assim fosse, haveria cargas em movimento dentro dele.
3) A linha de campo deve fazer um ângulo de 90º com a superfície do condutor. Caso contrário haveria uma componente tangencial, o que implicaria em ela não ser uma superfície equipotencial (obrigatório no equilíbrio eletrostático).
4) Não podem haver linhas de campo que saem da superfície do condutor e voltam até ela. Caso contrário ela não seria uma superfície equipotencial.
Passo 2
Agora vamos analisar as curvas uma a uma:
A curva 7 desobedece a regra 1, já q o condutor está carregado positivamente.
As curvas 1 e 4 desobedecem a regra 2.
As curvas 3 e 5 desobedecem a regra 3.
A curva 8 desobedece a regra 4.
Passo 3
Portanto, as linhas 1, 3, 4, 5, 7 e 8 não podem representar linhas de campo.
Alternativa correta é a letra (d).
Resposta
(d) 1, 3, 4, 5, 7 e 8.