UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 8c
Uma linha isolante de cargas tem a forma de um semicírculo de raio , como indicado na figura abaixo. Sua densidade linear de carga é dada por , onde é uma constante positiva e é o ângulo polar medido a partir do eixo .
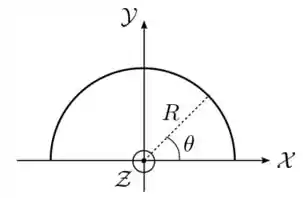
(c) Repita os dois itens acima, mas supondo agora que .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para calcular a carga total contida na linha de cargas que tem formato de semicírculo de raio :
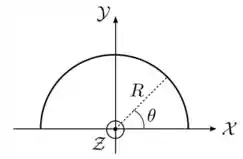
Para isso, temos que a carga total , primeiro temos que o elemento infinitesimal , que é dado por:
Onde é a densidade linear de cargas e é dada por .
Além disso, é o elemento infinitesimal da linha, que é dado por .
Agora, temos que substituir esses valores e integrar no semicírculo!!
E aí? Bora lá??!!
😉
Passo 2
Assim, substituindo os valores, encontramos a seguinte relação:
Logo, aplicando a integral no intervalo de a (que é o intervalo de um semicírculo), temos:
Nesse mesmo sentido, como a carga total é zero, então não há campo elétrico resultante no centro do semicírculo, ou seja:
Entendeu direitinho? Responde aee ;)
