Na figura, temos uma seção transversal de um corpo condutor, isolado (muito afastado de quaisquer outros corpos), em equilíbrio eletrostático carregado positivamente, além de algumas curvas orientadas. Quais curvas, nitidamente, não podem representar linhas de campo do correspondente eletrostático?
a) 1 e 4
b) 1, 4 e 7
c) 2, 6 e 7
d) 1, 3, 4, 5 e 7
e) 1, 3, 4 e 5
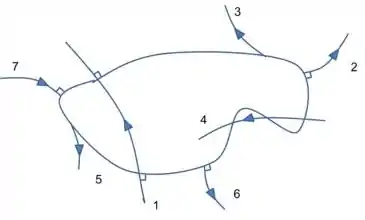
Passo 1
Com os dados do enunciado podemos concluir o seguinte
- O corpo é condutor e, portanto, não pode haver linhas dentro dele
- Carregado positivamente, portanto, as linhas de campo devem estar saindo deles
- Como o condutor é uma equipotencial, as linhas de campo devem ser perpendiculares a ele
Passo 2
Com essas informações, podemos concluir que somente as linhas 2 e 6 atendem esses requisitos, portanto, a resposta certa é a letra (d)
Resposta
(d)