Suponha que tenhamos duas cascas esféricas condutoras e concêntricas, onde a de menor raio tem uma carga positiva uniformente distribuída e a de maior raio tem uma carga negativa também uniformente distribuída.
Faça um esboço das linhas de campo elétrico:
I - Entre as duas cascas esféricas
II – Do lado de fora da casca esférica de maior raio
Considere os casos , e .
Passo 1
Primeiramente, devemos observar que os símbolos e usados no enunciado se referem ao valor absoluto das cargas.
Vamos analisar o primeiro caso: .
Temos que a carga na casca interna, é maior que a carga na casca externa, .
Como as linhas de campo elétrico saem das cargas positivas e entram nas negativas, as linhas de campo irão sair da casca interna na direção da casca externa.
Avaliando o campo elétrico do lado de fora da casca externa, o campo resultante será devido à soma das duas cargas. Como , a carga líquida total é positiva ( é negativo).
Portanto, as linhas de campo serão da seguinte maneira:
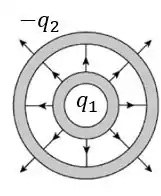
Obs.: podemos reparar que o campo do lado de fora da casca externa é menos intenso do que na parte interna (menos linhas linhas de campo), devido à carga líquida.
Passo 2
Agora vamos analisar o segundo caso: .
As linhas de campo na parte interna, serão iguais às do ítem anterior.
Porém a carga liquida nesse caso será zero.
E, assim, não haverá campo na parte de fora da casca externa.
Portanto, as linhas de campo serão da seguinte maneira:
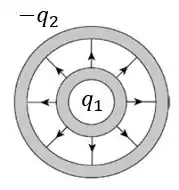
Passo 3
Agora vamos analisar o terceiro e último caso: .
As linhas de campo na parte interna, serão iguais às dos ítens anteriores.
Mas a carga líquida é diferente de zero e haverá um campo na parte de fora da casca externa.
Temos:
Assim, as linhas de campo na parte de fora da casca externa irão entrar na superfície (pois a carga líquida é menor que zero).
Portanto, as linhas de campo serão da seguinte maneira:
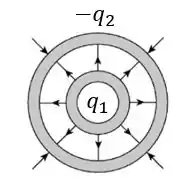
Obs.: podemos reparar que o campo do lado de fora da casca externa é menos intenso do que na parte interna (menos linhas linhas de campo), devido à carga líquida.
Resposta
Ei, a resposta está no passo a passo :)