Encontre a inversa da matriz abaixo, se existir:
Passo 1
Mais uma bem legalzona pra gente se divertir !!
Bom galerinha, esse se existir é importante, porque uma matriz só tem inversa quando seu determinante é diferente de zero !! Ou seja:
Para calcular o determinante nós vamos colocar as colunas e ao lado da matriz, desse jeito:
Depois nós vamos traçar linhas, da seguinte forma:
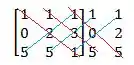
A multiplicação dos números ao longo das linhas vermelhas será positiva, enquanto as azuis negativas ! E para achar o determinante é só somar tudo:
Então, existe uma matriz inversa !!
Passo 2
Já vimos que a matriz inversa pode ser calculada colcando e quando transformamos A em identidade acharemos certo?
Então:
Para transformar A em sua forma reduzida, vamos começar zerando esse que está ali na primeira coluna:
Então:
Agora, precisamos transformar este em pivô, ou seja, em
Então:
Na coluna ainda temos que transformar o em zero:
Então:
Agora, precisamos fazer aparecer o pivô da terceira coluna:
Então:
E para finalizar daremos um jeitinho de zerar e
Então:
Quando nós chegamos neste ponto o que obtemos é:
Sendo assim,
Shoow de bolinhas !!