Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 140

140. A massa de 4   k g está suspensa pela mola de rigidez k = 350   N / m e está inicialmente em repouso na posição de equilíbrio. Se uma força para baixo F = C t é aplicada ao corpo e atinge um valor de 40   N quando t = 1   s , desenvolva a equação diferencial do movimento, obtenha a sua solução , e trace o deslocamento y em milímetros como uma função do tempo ao longo do primeiro segundo. O amortecimento é desprezível.

Passo 1

Primeiro, vamos montar o diagrama corpo livre da massa para a posição de equilíbrio:

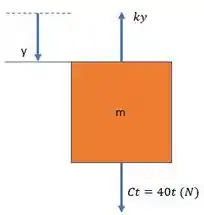
Passo 2

Agora, faremos o somatório de forças em y :

∑ F y = m y ¨

C t - k y = m y ¨

Lembrando que k y é a força elástica. Dividindo a expressão por m :

y ¨ + k m y = C t m

Mas temos que a frequência de ressonância ω n é dada por:

ω n 2 = k m

∴ y ¨ + ω n 2 y = C t m

Passo 3

Consideraremos y o deslocamento total:

y = y H + y P

Para y H teremos:

y H = A ⋅ c o s ω n t + B ⋅ s e n ( ω n t )

Agora, para y P = B 2 t em uma condição de equilíbrio:

0 + ω n 2 B 2 t = C t m

B 2 = C m ω n 2

Lembrando que ω n 2 = k m

B 2 = C k

∴ y = A ⋅ c o s ω n t + B ⋅ s e n ω n t + C t k

Ao rearranjarmos:

y = C k t - 1 ω n ⋅ s e n ( ω n t )

Passo 4

Agora, calculando C , sabemos que para t = 1   s , F = 40   N :

40   N = C × 1   s

∴ C = 40   N / s

Com k = 350   N / m e m = 4   k g , calcularemos ω n pela fórmula:

ω n = k m = 350   N / m   4   k g

∴ ω n = 9,35   r a d / s

Substituindo na equação de y :

y = 40   N / s 350   N / m t - 1 9,35   r a d / s ⋅ s e n ( 9,35   t )

∴ y = 114,3 [ t - 0,1069 ⋅ s e n 9,35 t ]

Resposta

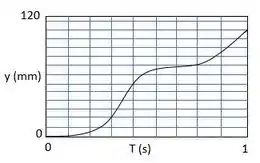
A equação do deslocamento y em função do tempo será:

y = 114,3 [ t - 0,1069 ⋅ s e n 9,35 t ]

E o gráfico será:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um oscilador harmônico amortecido é formado por um bloco ( m = 2,00k g ), uma mola ( k = 10,0N / m ) e uma força de amortecimento ( F = - b v ). Inicialmente, o bloco oscila com uma amplitude de 25,0c
A Amplitude de um oscilador fracamente amortecido diminui de 3,0 % a cada ciclo. Que percentagem da energia mecânica do oscilador é perdida em cada ciclo?
Em um oscilador amortecido com m = 250 g , k = 85 N / m e b = 70 g / s , qual é a razão entre a amplitude das oscilações amortecidas e a amplitude inicial após 20 ciclos?
Uma força de amortecimento Fx = -hvx atua sobre um rato infeliz de 0,300 kg que se move preso na extremidade de uma mola cuja constante é k = 2,50 N/m. (a) Se a constante b tem um valor igual a 0,900
Uma massa está vibrando na extremidade de uma mola com constante de força igual a 225 N/m. A Figura E13.62 mostra um gráfico de sua posição x em função do tempo t. (a) Em que momentos a massa não está