Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 76

Uma placa retangular uniforme é articulada em torno de um eixo horizontal que atravessa um de seus vértices conforme mostrado. Determine a frequência natural ω n para pequenas oscilações.

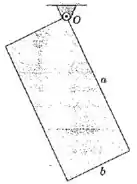
Passo 1

Vamos montar uma equação de momentos em relação ao ponto O :

∑ M O = I O θ ¨

A única força que produz momento em torno desse ponto é o peso da placa, agindo no seu centro de massa:

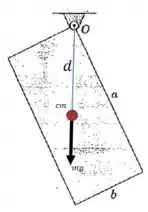
O momento dessa força peso segue a seguinte expressão:

∑ M O = - ( m g sen ⁡ θ ) ( d )

E a distância d pode ser calculada pelo teorema de pitágoras:

d = a 2 + b 2 2

Então:

∑ M O = - m g a 2 + b 2 2 sen ⁡ θ

Passo 2

Agora vamos olhar para o outro lado da equação:

∑ M O = I O θ ¨

Podemos usar o teorema dos eixos paralelos para encontrar o momento de inércia em relação ao ponto O :

I o = I c m + m d 2

I O = 1 12 m a 2 + b 2 + m a 2 + b 2 2 2

I O = 1 12 m a 2 + b 2 + 1 4 m a 2 + b 2   = 1 3 m a 2 + b 2

Então:

- m g a 2 + b 2 2 sen ⁡ θ = 1 3 m a 2 + b 2 θ ¨

Aproximando sen ⁡ θ ≅ θ e dividindo tudo por 1 3 m a 2 + b 2 :

θ ¨ + 3 g a 2 + b 2 2 a 2 + b 2 θ = 0

θ ¨ = 3 g 2 a 2 + b 2 θ = 0

E, como sempre, o termo que multiplica θ é o quadrado da frequência angular natural ω n que queremos calcular:

ω n 2 = 3 g 2 a 2 + b 2

ω n = 3 g 2 a 2 + b 2 - 1 4

Resposta

A frequência natural para pequenas oscilações é ω n = 3 g 2 a 2 + b 2 - 1 4 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

51. Se o coeficiente de amortecimento viscoso do amortecedor do Prob. 8 / 50 é c = 36 N ⋅ s / m , determine a faixa de frequência de excitação para a qual o módulo da resposta em regime permanente é i
59. Cada uma das esferas de 0,5k g está presa à extremidade da haste elástica leve e se desloca de 4m m quando uma força de 2N é aplicada estaticamente à esfera. Se o cursor central recebe um moviment
62. A unidade motorizada de 20k g com velocidade variável é limitada na direção horizontal por duas molas, cada uma das quais possui uma rigidez de 2,1k N / m . Cada um dos dois amortecedores possui u
48. Determine a amplitude X do movimento em regime permanente da massa de 10k g se (a) c = 500N ⋅ s / m e(b) c = 0 .
61. O movimento do carrinho externo B é dado por x B = b ⋅ s e n ω t . Para qual faixa da frequência d excitação ω , a amplitude do movimento da massa m em relação ao carrinho é inferior a 2 b ?