Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 17
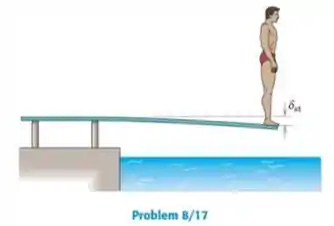
Um homem de está em pé na extremidade de um trampolim e provoca uma oscilação vertical que se observa ter um período de . Qual é a deflexão estática na extremidade do trampolim? Despreze a massa do trampolim.
Passo 1
Como o período das oscilações é dado, podemos calcular a frequência para a oscilação para determinarmos k para o trampolim, e então com ele calculamos a deflexão estática:
E a equação para a oscilação:
Ficamos com:
Isolando k:
Passo 2
Resolvendo utilizando o valor do período e da massa do homem:
Passo 3
Utilizando a equação de deflexão estática:
Substituindo os valores das grandezas:
Resposta
Exercícios de Livros Relacionados
42. A massa de um determinado sistema criticamente amortecido é liberada no instante de tempo t = 0 a partir da posição x 00 com uma velocidade inicial negativa. Determine o valor crítico ( x 0 ˙ ) c
41. O sistema apresentado é liberado a partir do repouso de uma posição inicialx 0 . Determine o deslocamento x 1 que ultrapassa a posição de equilíbrio. Assuma um movimento de translação na direção x
40. A massa de 2k g é liberada a partir do repouso a uma distância x 0 à direita da posição de equilíbrio. Determine o deslocamentox como uma função do tempo.
25. Na figura, está representado um modelo de um edifício de um andar. A barra de massa m é apoiada por duas colunas verticais elásticas leves, cujas extremidades superior e inferior estão impedidas d
46. Desenvolva a equação do movimento em termos da variável x para o sistema apresentado. Determine uma expressão para o fator de amortecimento ζ em termos das propriedades conhecidas do sistema. Desp