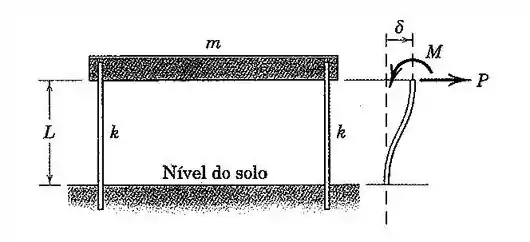
25. Na figura, está representado um modelo de um edifício de um andar. A barra de massa é apoiada por duas colunas verticais elásticas leves, cujas extremidades superior e inferior estão impedidas de girar. Para cada coluna, se uma força e o momento correspondente forem aplicados conforme indicado na parte à direita da figura, o deslocamento será dado por , onde é o comprimento efetivo da coluna, é o módulo de Young, e é o momento de inércia de área da seção transversal da coluna em relação a seu eixo neutro. Determine a frequência natural de oscilação horizontal da barra, quando as colunas se flexionam como mostrado na figura.
Passo 1
Bom, primeiro a gente vai montar o diagrama de corpo livre da barra:
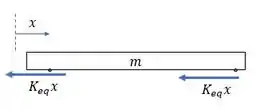
Onde é uma constante equivalente à uma constante de mola e o deslocamento de oscilação horizontal.
Passo 2
Como temos:
Podemos expressar a força na direção vertical em função das outras variáveis:
Essa força é equivalente à uma força elástica atuando, então:
Passo 3
Agora faremos o somatório de forças no eixo :
Onde é a aceleração em .
Rearranjando a expressão:
Sabemos que a equação genérica para um movimento harmônico:
Portanto:
E sabemos também que:
Resposta
A frequência de oscilação será: