Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.3 - Ex. 58

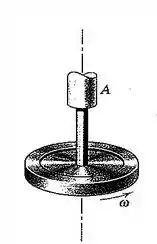
58. O disco circular de massa m está preso a um eixo elástico que está montado em um mancal rígido em A . Com o disco em repouso, uma força lateral P aplicada a ele produz uma deflexão lateral ∆ , de modo que a constante de mola equivalente é k = P / ∆ . Se o centro de massa do disco está deslocado do centro de uma pequena distância " e " a partir da linha de centro do eixo, determine a expressão para a deflexão lateral δ do eixo devida ao desbalanceamento a uma velocidade do eixo ω , em termos da frequência natural ω n = k / m de vibração lateral do eixo. A que velocidade crítica ω c a deflexão tenderia a se tornar grande? Despreze o amortecimento.

Passo 1

Bom, primeiro a gente vai fazer um diagrama pra ver o que está acontecendo no sistema:

Passo 2

Agora, vamos fazer o somatório de forças atuantes no disco:

∑ F = m a → n

Como só temos à força equivalente à força elástica e há rotação no disco, então a força equivalente à elástica será igualada à força centrípeta:

F e l . e q = F c p

k δ = m ( δ + e ) ω 2

Onde k é a constante de mola, δ a deflexão lateral, e o deslocamento do centro de massa do disco, m a massa do disco e ω a velocidade angular do disco.

k δ = m δ ω 2 + m e ω 2

k δ - m δ ω 2 = m e ω 2

Isolando δ :

δ k - m ω 2 = m e ω 2

δ = m e ω 2 k - m ω 2

Passo 3

Podemos arrumar a equação se lembrarmos que:

ω n = k m

ω n 2 = k m

Dividindo o segundo membro da equação de δ em cima e embaixo por k :

δ = m e ω 2 k k - m ω 2 k

δ = e ω 2 ω n 2 1 - m ω 2 k

δ = e ω ω n 2 1 - ω 2 ω n 2

δ = e ω ω n 2 1 - ω ω n 2

Passo 4

A velocidade crítica ω c será dado para:

ω c = k m

Porque, assim:

ω ω n = 1

E o denominador da equação do δ seria 0 , o que faria o δ ir para o infinito.

Resposta

Expressão de δ :

δ = e ω ω n 2 1 - ω ω n 2

E a velocidade angular crítica ω c :

ω c = k m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para um oscilador de massa m , frequência livre ω 0 e constante de amortecimento γ , sujeito à força externa F = F 0 cos ⁡ ω t , calcule: (a) O valor exato de ω para o qual a amplitude de oscilação es
Seja x = a cos ⁡ ω t + b sen ⁡ ω t a solução estacionária para o movimento de um oscilador amortecido sob a ação da força F = F 0 cos ⁡ ω t . Mostre que somente a componente em quadratura contribui pa
Duas partículas de mesma massa, igual a 250g , estão suspensas do teto por barras idênticas, de 0,5m de comprimento e massa desprezível, e estão ligadas uma à outra por uma mola de constante elástica
Uma pessoa está segurando uma extremidade A de uma mola de massa desprezível e constante elástica 80N / m . Na outra extremidade B , há uma massa de 0,5k g suspensa, inicialmente em equilíbrio. No ins
Dois pêndulos idênticos, formados por partículas de massa m suspensas por barras de massa desprezível e comprimento l , estão ligadas um ao outro por uma mola de massa desprezível e constante elástica