(Adaptada) Um bocal venturi moderno é calibrado em um escoamento de laboratório com água a 20°C. O diâmetro do tubo é 5,5 cm, e o diâmetro da garganta do venturi é 3,5 cm. A vazão é medida por meio de um tanque de pesagem e a queda de pressão por meio de um manômetro de água e mercúrio. A vazão em massa e as leituras manométricas são as seguintes:

Use esses dados para plotar uma curva de calibração do coeficiente de descarga do venturi em função do número de Reynolds. Compare com a correlação aceita.
Equação de correlação para o medidor Venturi moderno
Dados: , e
Passo 1
E aííí! Nesse exercício, já temos valores de vazão. O que viemos fazer aqui então? Analisaremos vários pontos para encontrar a curva do coeficiente de descarga C.
O enunciado deu a cruva esperada, a aceita, mas lá vamos nós verificar se com o experimento feito, esse comportamento da curva é realmente atingido 😉
O que foi fornecido? Vazão mássica em kg/s, já está no Sistema Internacional, show de bola! E foi fornecido a leitura do manômetro de água e mercúrio, em milímetros. Isso vai ajudar a calcular a queda de pressão Δp que o medidor venturi está provocando nesse escoamento
Como o fluido em escoamento é a água e o que está nos ajudando a medir a pressão é o mercúrio, faremos assim:
Substituindo os dados do enunciado
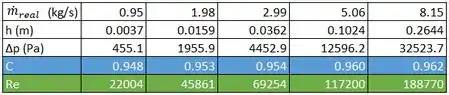
Então, com essa equação, podemos acrescentar mais uma linha para aquela tabela. Temos a leitura h de cada experimento, então vamos multiplicar cada uma delas por 123009,6 para encontrar cada diferença de pressão 😉
Lembrando que para achar Δp em Pascal, vamos usar as alturas h em metros, certo? Já atualizando isso na tabela

Além da tabela, o enunciado forneceu os diâmetros do tubo e da garganta do Venturi, então podemos calcular a razão β
Beleza, os dados estão organizados, então vamos lá ao cálculo de C
Passo 2
Para calcular C, vamos nos lembrar que estamos em medição de vazão. Então, essa fórmula aqui nos ajuda
A área da garganta é e como o diâmetro do venturi é fixo (o mesmo para todos os pontos do experimento:
Isolando C, que é quem queremos calcular
A razão β e a massa específica ρ também são fixos em todos os pontos, pois é o mesmo medidor e mesmo fluido em escoamento (água) sendo analisados. Então
Fazendo as contas das constantes
Na nossa tabela atualizada, para cada valor de vazão mássica real, temos o valor da diferença de pressão Δp provocada pelo medidor. Yay!
Então para cada par de pontos , vamos encontrar um valor para o coeficiente de descarga C
Com isso, vamos acrescentar mais uma linha na tabela, usando essa expressão que encontramos

Esses são os valores do coeficiente de descarga para cada ponto :D
Passo 3
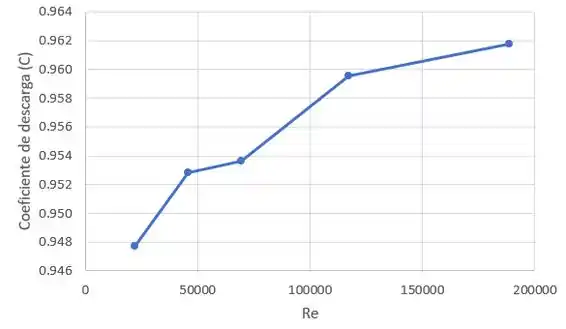
O exercício pede para plotarmos uma curva do coeficiente de descarga C versus o Reynolds.
Vamos então calcular Reynolds, que é
Mas, como não foi dada a velocidade, vamos reescrevê-la em função da vazão volumétrica, já que
Além disso, não temos a vazão volumétrica, mas temos a vazão mássica. Como e
Com isso, atualizando Reynolds
Simplificando
Substituindo e que não mudam nesse experimento
Então, encontramos uma expressão para Reynolds
Isso significa que para cada vazão mássica diferente, o valor de Reynolds será diferente e calculado por essa expressão. Vamos lá adicionar mais uma linha na nossa tabela
E agora vamos plotar a curva do coeficiente de descarga C em função do Reynolds, como o exercício pediu :DD
Passo 4
Vamos comparar com a correlação aceita
Repara que essa correlação não depende de Reynolds! Mas, relaxa, não fizemos todos esses cálculos em vão. É que essa correlação é válida para uma faixa de Reynolds bem curtinha, de
E nossos dados, vão de até . Só o último ponto dos nossos dados está dentro da validade dessa correlação. Então vamos ver se ele tá compatível!
Calculando o C pela correlação e substituindo β = 0,64
Para , encontramos C = 0,962. O valor está próximo, então está coerente!
Para fazer uma correlação válida para valores menores de Reynolds, precisaríamos usar os pontos que calculamos no passo anterior e fazer um ajuste, encontrando a equação mais adequada. O número de Reynolds teria que entrar nessa equação 😉
Resposta
Ei, a resposta está no passo a passo :)