Etanol a 20°C escoa para baixo por um bocal venturi moderno, como na figura. Se o manômetro de mercúrio indica 100 mm, como mostrado, calcule vazão em L/min.
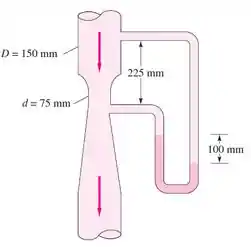
Dados: , e
Equação de correlação para o medidor Venturi moderno
Passo 1
Vamos lá! Esse exercício pede para calcularmos a vazão volumétrica usando um bocal venturi moderno.
Pela figura, podemos encontrar o , que é e pelos nomes dados às variáveis na figura:
Além disso, a pressão está sendo medida por um manômetro de mercúrio (Hg). Então aqueles 100 mm indicados na figura mostram que a diferença de pressão provocada pelo venturi é
Ou seja, é a pressão da coluna de 100 mm de mercúrio menos a pressão da coluna de 100 mm de etanol
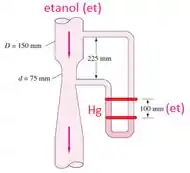
Substituindo
Então, a diferença de pressão medida pelo manômetro é de
São conhecidos: Δp, ρ (do fluido escoando, que é o etanol) e β
Passo 2
Para calcular a vazão volumétrica, está faltando conhecer o coeficiente de descarga C. Mas antes, vamos reorganizar a equação da vazão mássica
Como e
Lembrando que aqui, a massa específica é a do etanol, pois ele é o fluido em escoamento!
E para encontrar o coeficiente de descarga, como o medidor de vazão é um Venturi moderno e conhecemos a razão entre os diâmetros, podemos usar essa correlação
Substituindo
Encontramos o coeficiente de descarga! Estamos quase lá!
Passo 3
Vamos encontrar essa vazão então! Usando a fórmula que já desenvolvemos da própria vazão
Substituindo os valores encontrados *-* (lembrando que a massa específica é do etanol! O mercúrio só nos ajudou a medir a diferença de pressão.)
Como a vazão volumétrica foi pedida em L/min, vamos converter
Medimos a vazão 😉