Gasolina a 20°C escoa a por um tubo de 15 cm de diâmetro e é medida por um medidor do tipo bocal de raio longo de 9 cm. Qual é a queda de pressão esperada através do bocal?
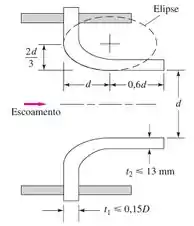
Passo 1
Vamos lá! Nesse exercício temos um medidor de vazão que é um bocal! Queremos calcular a a queda de pressão Δp. E quem já sabemos pelo enunciado?
“Tubo de 15 cm de diâmetro” significa que o diâmetro antes da medição é de 15 cm

Quando o enuciado fala “medidor do tipo bocal de raio longo de 9 cm”, sabemos que
Sabendo e , podemos calcular a razão β
Finalmente, para completar os dados: o fluido é a gasolina a 20°C, logo
Passo 2
Para calcular o Δp, utilizamos essa fórmula em medidores de vazão
Lembrando que e
Para calcular o valor de C, vamos usar a equação de correlação para bocais de raio largo.
Essa equação é válida para β entre 0,25 e 0,75 (é o nosso caso, pois nosso β é 0,6) e para entre e (precisamos calculá-lo e conferir!)
A velocidade não costuma ser dada (e nesse exercício não foi mesmo...) Maaas, vamos usar a fórmula da vazão volumétrica, que vai nos salvar :D
Logo
Substituindo os valores
Eba! Está dentro do intervalo e assim podemos usar a correlação! Uhul!
Substituindo Reynolds e β na correlação
Logo,
Finalmente, podemos substituir na equação da vazão mássica. :D
Passo 3
A gente tinha arrumado a equação da vazão mássica real desse jeito
Substituindo os valores que encontramos
Fazendo as contas
Logo, é a queda de pressão esperada pelo bocal!