Gasolina a 20°C escoa a em um tubo de 10 cm de diâmetro. Desejamos medir a vazão com uma placa de orifício e um transdutor de pressão diferencial que fornece as melhores leituras a cerca de 55 kPa. Qual é a razão β adequada para o orifício?
Dados: e
Passo 1
Nesse exercício, nosso medidor de vazão é uma placa de orifício. Olha ela aí
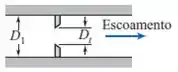
Só que ao invés de querer descobrir a vazão ou a diferença de pressão, o enunciado pede a razão β, ou seja
Vamos organizar o que o enunciado deu, passando tudo para o Sistema Internacional. Primeiramente, foi dada a vazão volumétrica Q
O diâmetro do tubo é de 10 cm, ou seja
Além disso, quando o enunciado diz que o “transdutor de pressão diferencial que fornece as melhores leituras a cerca de 55 kPa”, podemos escrever que
Além disso, como conhecemos o fluido, que é a gasolina e sabemos a sua massa específica a 20°C, então podemos calcular a vazão mássica
Passo 2
Na teoria, vimos que a expressão da vazão mássica real é
ou
Como queremos encontrar a razão β, vamos usar a primeira! 😊 Nela, já conhecemos a vazão mássica, a massa específica e a diferença de pressão. Ainda não conhecemos sobre a geometria e sobre o C, o coeficiente de descarga.
Para achar C, precisamos do número de Reynolds antes da medição da vazão.
Por sua vez, a velocidade é vazão volumétrica sobre área, então ficamos com as contas assim:
Simplificando
Substituindo os valores
A partir desse Reynolds, podemos consultar o gráfico C x Re
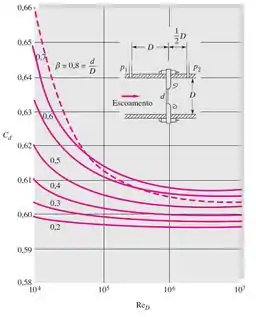
Repara que no número de Reynolds encontrado, todas as curvas associadas à razão β, fornecem resultado de coeficiente de descarga C próximo a 0,61
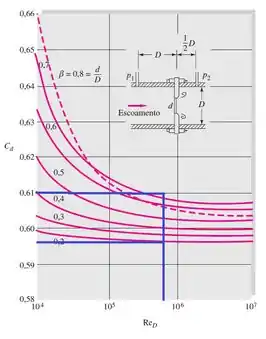
Assim, vamos utilizar esse valor na fórmula da vazão mássica para encontrar o β
Passo 3
Reescrevendo a equação da vazão mássica
Além disso, essa pode ser escrita em função de β, já que
Substituindo na equação da vazão mássica
Substituindo os valores dados no enunciado e os encontrados até aqui
Fazendo as contas
Elevando ao quadrado os dois lados da equação
A razão entre os diâmetros da garganta e o inicial é 0,66.