Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Medidores de vazão: orifício, bocal e venturi

Ver Teoria
Exercício 61234578

Enunciado

Água a 65°C escoa através de um orifício com diâmetro de 75 mm instalado em um tubo de 150 mm de diâmetro interno. A vazão é 20 L/s. Determine a diferença de pressão entre as tomadas de canto.

ρ á g u a   65 º C = 980 k g / m 3

μ á g u a   65 º C = 4,3 . 10 - 4 k g / ( m . s )

Passo 1

Faaaaala! Começamos aqui nossos exercícios de medidores de vazão e este aqui quer saber a diferença de pressão ∆ p . Show de bola!

Logo no início, o enunciado fala que nosso medidor de vazão é do tipo orifício. Ou seja, é nesse estilo:

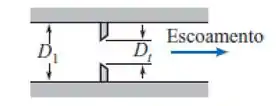
Além disso, foi o diâmetro do orifício ( D t ) e o diâmetro do tubo ( D 1 ). Assim, conseguimos encontrar a razão β

β = D t D 1 = 75   m m 150   m m = 0,5

Também foi dada a vazão, que é 20 L/s. Repara que essa é a vazão volumétrica Q, pelas unidades de volume por tempo. No Sistema Internacional:

Q r e a l = 0,02   m 3 / s

Passo 2

Para encontrar a diferença de pressão em um medidor de vazão de restrição (que é o caso, pois é de orifício), usamos a seguinte fórmula

m ˙ r e a l = K A t 2 ρ p 1 - p t

Mais especificamente

m ˙ r e a l = K A t 2 ρ ∆ p

Nesse exercício foi dada a vazão volumétrica e não a mássica! Por isso, vamos usar

m ˙ r e a l = ρ Q r e a l

Substituindo os dados do enunciado

m ˙ r e a l = 980 × 0,02 = 19,6   k g / s

Além disso, A t = π D t 2 / 4  

A t = π 0,075 2 / 4 ≅ 0,004416   m 2

Logo, para calcular a diferença de pressão, só falta conhecer o coeficiente de vazão K

m ˙ r e a l = K A t 2 ρ ∆ p

19,6 = K × 0,004416 × 2 × 980 × ∆ p

Passo 3

Para calcular K, precisamos calcular o número de Reynolds antes da medição, isto é, R e D 1

R e D 1 = ρ V 1 D 1 μ

Não foi dada a velocidade, mas foi dada a vazão volumétrica, então vamos usar sua definição

Q = V A   ⇒ V = Q A

V 1 = Q A 1 =   0,02 π D 1 2 / 4

V 1 = 0,02 π 0,150 2 / 4 = 1,13   m / s

Assim, podemos calcular o número de Reynolds :D

R e D 1 = 980 × 1,13 × 0,150 4,3 . 10 - 4

R e D 1 = 3,9 . 10 5

Opa! Estamos quase lá! Na teoria, vimos que podemos usar esse gráfico aqui para calcular K em placas de orifício

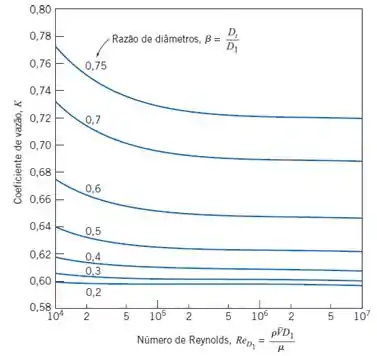
Conhecemos Reynolds, e ele é aproximadamente 4 × 10 5 e sabemos que β = 0,5 . Utilizando esses pontos no gráficos, temos que...

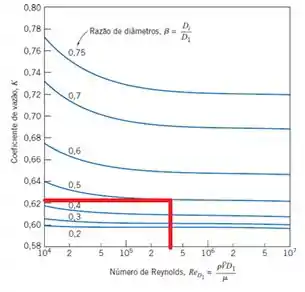
...K é aproximadamente 0,624

Substituindo esse valor na fórmula da vazão mássica real que desenvolvemos até agora

m ˙ r e a l = K A t 2 ρ ∆ p

19,6 = 0,624 × 0,004416 × 2 × 980 × ∆ p

2 × 980 × ∆ p = 7112,8

Elevando os dois lados da equação ao quadrado

2 × 980 × ∆ p = 50592348

∆ p = 25812,4   P a

Logo, a diferença de pressão é de ∆ p = 25 , 8   k P a

Resposta

∆ p = 25,8   k P a

Exercícios de Livros Relacionados

Um pequeno objeto pesa 6 N no ar e 4,6 N quando mergulhado num líquido. O volume do objeto é 170 cm³. Qual é a massa específica, o peso específico e o peso específico relativo do líquido, se o peso es
Um densímetro é constituído de um cilindro de 0,5 cm de diâmetro e 36 cm de altura. No fundo do cilindro está presa uma esfera de 2,5 cm de diâmetro. O dispositivo pesa 0,15 N. Qual é a altura do cili
Uma esfera de chumbo ( γ = 1,14.10 5N / m 3 ) , de 0,5 cm de diâmetro, cai numa coluna de óleo ( γ = 8600N / m 3 ) com uma velocidade de 0,05 m/s. Determinar a viscosidade do óleo.
8.203Canudinhosderefrigerantepodemserusadosparamelhoraroescoamentodearemumexperimento.Opreenchimentodeum trechodotubocomcanudos,demodoaformarum“elementodeescoamentolaminar”,poderiapermitiramediçãodire
As perdas na válvula borboleta da figura 6.19b podem ser associadas a um tipo de dispositivo de obstrução de Bernoulli, como na figura 6.39. A área da garganta, Ag na equação 6.104 pode ser interpreta