(Adaptada) Deseja-se medir um escoamento de gasolina a 20°C em um tubo de 12 cm de diâmetro, usando um bocal venturi moderno. Para que os padrões internacionais sejam válidos, tais como no gráfico a seguir, qual é a gama admissível de (a) vazões, (b) diâmetros do medidor e (c) quedas de pressão.
Passo 1
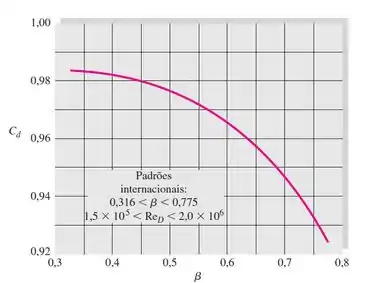
Vamos avaliar esse medidor de vazão do tipo venturi! A figura do exercício traz os padrões internacionais, e eles são:
Sabemos também pelo enunciado que o diâmetro do tubo
E como o fluido é a gasolina a 20°C, então
A partir dos padrões internacionais de Reynolds, conseguiremos encontrar a faixa de vazões admissíveis. Isso porque, pela definição de Re
E como
Essa área 1 também pode ser desenvolvida
E ficamos com o Reynolds em função da vazão
Substituindo os valores da gasolina e do bocal venturi estudado
Como conhecemos a faixa de Reynolds pelos padrões internacionais
Escrevendo Reynolds em função da vazão volumétrica, encontramos a gama admissível de vazões
Letra a feita!
Passo 2
A letra b pede a faixa de diâmetros do medidor. Pelos padrões internacionais, temos a faixa de
E como é a razão entre os diâmetros e nós sabemos que o medidor é usado num tubo de 0,12 m de diâmetro:
Reescrevendo o padrão internacional de com essa expressão
Multiplicando todo mundo por 0,12
Essa é a gama de diâmetros do medidor bocal venturi admissível! Yay!
Passo 3
Para saber a faixa de Δp admissíveis nesse medidor, vamos usar a equação na qual essa variável está
Vamos reorganizar ela para ficarmos com variáveis que foram dadas nesse exercício, ok? Por exemplo, vamos transformar essa vazão mássica em vazão volumétrica usando
Além disso,
Atualizando a equação da vazão
Como o fluido é a gasolina, vamos substituir o
Já que queremos saber a faixa de Δp, então, vamos colocar só ele de um lado da equação (mas vamos com calma)
A diferença de pressão depende de β, Q e C. Sabemos as faixas de β e Q possíveis, mas não sabemos ainda o coeficiente de descarga. Para isso, vamos usar o gráfico mostrado no enunciado.
O gráfico é de C e função de β. Usando o menor e o maior valor de β admissíveis, encontraremos a faixa de C
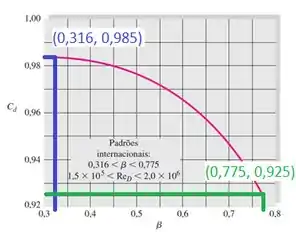
Logo, para e para
Além disso, quanto maior o , maior é o diâmetro do medido e consequentemente, menor é a vazão Q. Então para o maior , usaremos a menor vazão Q
Substituindo esses valores na fórmula da vazão
No mesmo raciocínio, o menor corresponde a maior vazão Q
Substituindo
Logo, a gama de diferença de pressão é
E encontramos tudo! Vamos para o próximo exercício? o/
Resposta
(a)
(b)
(c)