Considere o seguinte sistema de equações lineares:
Mostre que este sistema não satisfaz o critério de linhas;
Mostre que esse sistema não satisfaz o critério de Sassenfeld;
O que se pode afirmar sobre a convergência dos métodos de Gauss-Jacobi e Gauss-Seidel, quando aplicados a este sistema?
Mostre que o sistema obtido permutando-se as duas primeiras equações satisfaz o critério de Sassenfeld;
Passo 1
(a) Vamos relembrar como funciona o critério das linhas?
Vamos calcular um para cada linha da matriz e verificar se o maior desses ’s é menor do que 1. Se o maior dos ’s for menor do que 1, o critério das linhas é satisfeito e o método irá convergir.
Tá... na teoria ta lindo, mas como calculamos esses ’s?
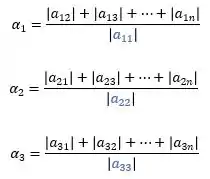
Verificando o critério das linhas:
Só pelo já podemos ver que ele não satisfaz o critério.

Passo 2
(b) Da mesma forma, verificando o critério de Sassenfeld:
Novamente, apenas pelo valor de já sabemos que o critério não é satisfeito.
(c) Nesse caso não podemos afirmar nada a respeito da convergência dos métodos de Gauss-Jacobi e Gauss-Seidel quando aplicados a esse sistema. Eles podem convergir ou divergir.
Passo 3
(d) Permutando-se as duas primeiras linhas obtemos:
Verificando o critério de Sassenfeld:
Logo, . Então, o sistema satisfaz o critério de Sassenfeld.

Resposta
Ei, a resposta está no passo a passo :)