Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método de Romberg

Exercício 31245678910

Enunciado

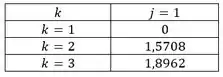
Utilize o conteúdo aprendido para realizar o primeiro passo da Integração de de Romberg para obter uma aproximação para a integral abaixo com k = 1,2 , 3   .

I = ∫ 0 π s e n x d x

Passo 1

Opa!! Vamos relembrar um pouco sobre o método de Roberg para atacar esse exercício?

Basicamente o Método de Romberg consiste na sucessiva aplicação da extrapolação de Richardson à uma quadratura composta de maior exatidão.

A determinação da integral é dada por:

I ≅ ∫ a b f x d x = h k 2 [ f a + f b + 2 ∑ i = 1 2 k - 1 f ( a + i . h k ) ]

Onde:

h k = b - a 2 k - 1

Aqui, h k representa a amplitude entre cada subintervalo.

Passo 2

Beleza... mas quem é R 1,1 ?

A primeira coisa que iremos fazer para resolver a integral é definir uma nova notação:

R k , j

Onde:

k = 1,2 , … , n

j = 1,2 , … , k

Aí meus caros, temos que ter um valor inicial... certo?

Primeiro quando k = 1 :

R 1,1 = h k 2 f a + f b

Generalizando para k = 2,3 , … , n ficamos com:

R k , 1 = 1 2 [ R k - 1,1 + h k - 1 [ ∑ i = 1 2 k - 2 f ( a + 2 i - 1 h k ) ]

Aqui queremos calcular para k = 1 ,   2   e   3 , certo?!

Passo 3

Para k = 1 :

R 1,1 = ( b - a ) 2 f a + f b

R 1,1 = ( π - 0 ) 2 s e n ( π ) + s e n ( 0 )

R 1,1 = 0

Para k = 2 :

R k , 1 = 1 2 [ R k - 1,1 + h k - 1 [ ∑ i = 1 2 k - 2 f ( a + 2 i - 1 h k ) ]

R 2,1 = 1 2 [ R 1,1 + h 1 . f a + h 2 ]

h k = b - a 2 k - 1

h k = b - a 2

R 2,1 = 1 2 [ R 1,1 + b - a . f a + b - a 2 ]

R 2,1 = 1 2 [ 0 + π - 0 . s e n 0 + π - 0 2 ]

R 2,1 = 1 2 [ π . s e n π 2 ]

R 2,1 = π 2 = 1,5708

Passo 4

Para k = 3 consideramos :

R k , 1 = 1 2 R k - 1,1 + h k - 1 ∑ i = 1 2 k - 2 f ( a + 2 i - 1 h k )

R 3,1 = 1 2 R 2,1 + h 2 . f a + h 3 + f a + 3 . h 3

R 3,1 = 1 2 R 2,1 + h 2 . f a + h 3 + f a + 3 . h 3  

Quem vai ser h 3 aqui??

Utilizaremos a fórmula

h 3 = b - a 2 k - 1 = b - a 4

Beleza?! Agora, substituindo

R 3,1 = 1 2 R 2,1 + b - a 2 . f a + b - a 4 + f a + 3 . b - a 4

R 3,1 = 1 2 R 2,1 + π - 0 2 . f 0 + π - 0 4 + f 0 + 3 . π - 0 4

R 3,1 = 1 2 R 2,1 + π - 0 2 . f 0 + π - 0 4 + f 0 + 3 . π - 0 4

R 3,1 = 1 2 1,5708 + π 2 . f π 4 + f 3 . π 4

R 3,1 = 1 2 1,5708 + π 2 . s e n π 4 + s e n 3 . π 4

R 3,1 = 1,8962

Resposta