Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Modelos e Efeitos da Temperatura

Ver Teoria
Exercício 123456789

Enunciado

A figura abaixo apresenta 2 experimentos realizados para estudar graficamente a Equação de Arrhenius.

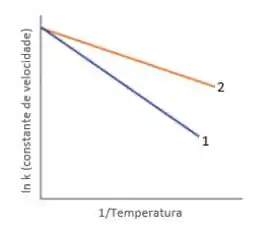
  1. As duas retas representam reações diferentes. Como podemos provar isso?
  2. Qual das duas reações tem uma maior energia de ativação?

Passo 1

Esse exercício é super importante para entendermos como funcionam os gráficos que descrevem a equação de Arrhenius!

Vamos lembrar a equação:

ln ⁡ k = ln ⁡ A -   E a R T

Se pensarmos que, para uma mesma reação, A e E a são praticamente invariáveis com a temperatura e que R é uma constante, podemos pensar na equação como: ln ⁡ k   ( e i x o   y ) = ln ⁡ A   o n d e   a   r e t a   c o r t a   o   g r á f i c o -   E a R i n c l i n a ç ã o   d a   r e t a . 1 T ( e i x o   x )

Com isso na cabeça, bora resolver o que o enunciado pede.

Passo 2

a) Sobre a inclinação da reta:

A gente acabou de ver que a inclinação das retas representam - E a / R . Como R é uma constante, o que vai mudar de uma reta para outra é a energia de ativação. A energia de ativação é própria de uma reação, cada reação vai ter a sua. Se duas reações tem inclinações diferentes, elas vão ter energias de ativação diferentes, sendo, assim, duas reações diferentes!

Passo 3

b) Mais uma vez o enunciado tá perguntando sobre a energia de ativação, então temos que olhar pra inclinação da reta.

Ter uma energia de ativação maior significa que o termo E a / R vai ser maior. Logo, a reta “cai mais rápido”, tem uma maior inclinação. Qual reta tem maior inclinação?

Se você pegar um intervalo de 1 / T vai ver que o ln ⁡ k varia mais para a reta azul do que pra vermelha, o que significa que ela tem uma inclinação maior! Logo a reta azul representa uma reação com maior energia de ativação!

Resposta

  1. Podemos provar através das diferentes inclinações na reta (o que indica energias de ativação diferentes).
  2. A reta azul (número 1)

Exercícios de Livros Relacionados

Use programas de computação gráfica padronizados para fazer o gráfico de Arrenius apropriado aos dados mostrados aqui para a decomposição do iodo-etano em eteno e iodeto de hidrogênio, C 2 H 5 I g → C
A constante de velocidade da reação O g + N 2 g → N O g + N ( g ) , que ocorre na estratosfera, é 9,7 × 10 10 L ⋅ m o l - 1 ⋅ s - 1 , em 800º C º . A energia de ativação da reação é 315k J ⋅ m o l - 1
Na reação reversível, em uma etapa, A + B⇌ C + D , a constante de velocidade da reação direta é 52,4L ⋅ m o l - 1 ⋅ h - 1 e da reação inversa é 32,1L ⋅ m o l - 1 ⋅ h - 1 . A energia de ativação da rea
A constante de velocidade da reação de segunda ordem 2 H I g → H 2 g + I 2 g é2,4 × 10 - 6L ⋅ m o l - 1 s - 1 é em 575 K , e 6,0 × 10 - 5L ⋅ m o l - 1 ⋅ s - 1 , em630 .K . Calcule a energia de ativaçã
O etano, C 2 H 6 , se dissocia em radicais metila, em 700 . º C º , com constante de velocidade k = 5,5 × 10 - 4 s - 1 . Determine a constante de velocidade, em 800 .º C º , sabendo que a energia de a