Exercícios Resolvidos de Modelos e Efeitos da Temperatura

Enunciado

A reação química entre acetato de etila e o íon hidroxila produzindo etanol e o íon acetato, foi estudada em diversas temperaturas, conforme mostrado abaixo.

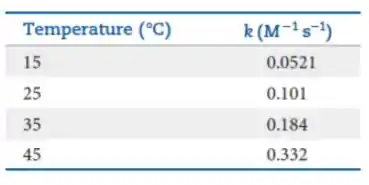
Pede-se:

Determine o valor da energia de ativação e do fator pré-exponencial.

Estime o valor da constante de velocidade na temperatura de .

Passo 1

a) Relembrando a equação de Arrhenius:

Aplicando ln dos dois lados:

Aí tem duas formas de fazer: a primeira é por regressão linear, usando todos pontos, e a segunda é usando só duas temperaturas ali de cima, pra resolver por sistema.

Relaxa que vamos fazer juntos dos dois jeitos.

Passo 2

Pra fazer por regressão linear:

Repara que essa equação daqui:

É uma reta!

Então se você traçar os valores de versus os valores de vai encontrar uma reta de coeficiente linear igual a e coeficiente angular igual a .

A gente começa por calculando os valores de x e y a partir da tabela dada:

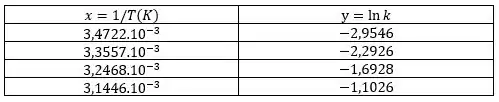
Aí você vai fazer uma regressão linear com esses dados na calculadora científica, que já te dá direto os valores de coeficiente linear e angular da reta formada pelos pontos que você informou pra ela.

Fazendo isso, vamos encontrar:

O que só nos confirma que os dados realmente formam uma reta!

Como:

Então:

E, dado que:

Vamos ter:

Esse método é “mais correto” porque utiliza todos os pontos dados. Você só precisa tomar cuidado com as unidades: vai ter a mesma unidade do seu e vai ter unidades dependendo do seu . Aqui usamos , por isso que nossa ficou nessa unidade.

Agora se regressão linear não é com você, você pode usar apenas dois pontos pra encontrar os valores de e . Pega o passo 3 aí.

Passo 3

Agora vamos precisar de dois pontos quaisquer. Vamos escolher os pontos onde e .

Passando essas temperaturas para , temos:

Substituindo os valores de e na equação de Arrhenius:

Organizando, obtemos:

Subtraindo a 2ª equação da 1ª :

Que equivale a:

Substituindo na primeira equação do sistema:

Repara que tem que ter a mesma unidade que , já que o termo da exponencial necessariamente não tem unidade e:

Passo 4

b) Agora que já temos e , já podemos calcular o para ():

Usando os valores encontrados pela regressão linear:

Assim, o de é . Se a gente olhar na tabela, esse valor está entre os valores de para e , o que é coerente.

Resposta

Energia de ativação =

Exercícios de Livros Relacionados

Use programas de computação gráfica padronizados para fazer o gráfico de Arrenius apropriado aos dados mostrados aqui para a decomposição do iodo-etano em eteno e iodeto de hidrogênio, C 2 H 5 I g → C

A constante de velocidade da reação O g + N 2 g → N O g + N ( g ) , que ocorre na estratosfera, é 9,7 × 10 10 L ⋅ m o l - 1 ⋅ s - 1 , em 800º C º . A energia de ativação da reação é 315k J ⋅ m o l - 1

Na reação reversível, em uma etapa, A + B⇌ C + D , a constante de velocidade da reação direta é 52,4L ⋅ m o l - 1 ⋅ h - 1 e da reação inversa é 32,1L ⋅ m o l - 1 ⋅ h - 1 . A energia de ativação da rea

A constante de velocidade da reação de segunda ordem 2 H I g → H 2 g + I 2 g é2,4 × 10 - 6L ⋅ m o l - 1 s - 1 é em 575 K , e 6,0 × 10 - 5L ⋅ m o l - 1 ⋅ s - 1 , em630 .K . Calcule a energia de ativaçã

O etano, C 2 H 6 , se dissocia em radicais metila, em 700 . º C º , com constante de velocidade k = 5,5 × 10 - 4 s - 1 . Determine a constante de velocidade, em 800 .º C º , sabendo que a energia de a