Dividindo o polinômio por o quociente e o resto
Com esses dados utilize o Matlab e obtenha a
Passo 1
Opa galerinha, aqui estamos em um exercício de divisão de polinômios.
O problema deseja encontrar um polinômio que segundo o enunciado é o resultado da seguinte operação:
Logo multiplicando toda a equação pelo , temos:
Ou seja, o problema se torna basicamente uma multiplicação de polinômios que pode ser resolvido utilizando a função que é utilizada para realizar a multiplicação dos polinômios.
Primeiramente para a resolução da questão precisamos implementar os vetores dos coeficientes dos polinômios.
Com isso podemos utilizar a função e encontrar a .
Sendo assim, o algoritmo se torna:
1-Implementar o vetor dos coeficientes dos polinômios.
2-utilizar a função conv para realizar as operações
3-Analisar o resultado.
Passo 2
Agora que criamos nosso algoritmo vamos implementá-lo no Matlab.
Primeiramente vamos começar inserindo os vetores dos coeficientes dos polinômios e
Aqui o zero aparece pois não existe o coeficiente linear, logo colocamos o zero para indicar que existe apenas o termo quadrático e linear no x.
Realizando a multiplicação temos:
A saída da função conv é o produto dos polinômios, enquanto sua entrada é os vetores com os coeficientes dos polinômios.
A ordem de inserção nessa função não importa, ou seja:
Digitando tudo certinho no command windows do Matlab deve gerar algo assim:
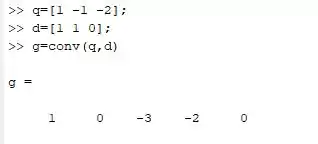
Ou seja, temos um polinômio de grau 4, para somar com o resto precisamos completar o polinômio do resto até ele atingir o grau 4.
Pois só podemos somar vetores se tiver o mesmo número de elementos, colocando até chegar no grau 4 temos que o resto se torna:
Realizando a soma o polinômio se torna:
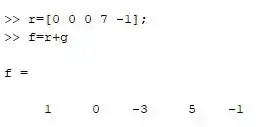
Resposta
Sendo assim o polinômio final é: