Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Operações com Polinômios (Zeros, Soma, Produto e Divisão de Polinômios)

Ver Teoria
Exercício 71234568

Enunciado

Se R ( x ) é o resto da divisão do polinômio P x = x 4 - 3 x 3 + 2 x - 3 pelo polinômio D x = x + 1 , então o valor de R ( x ) é?

Passo 1

Para resolver essa questão vamos precisar lembrar da formulazinha da divisão de polinômios, que é dada por:

P ( x ) D ( x ) = Q x + R x D ( x )

Ou seja, nosso problema aqui se resume a uma divisão de dois polinômios.

Para resolver qualquer questão de polinômios o tópico mais importante é a inserção dos vetores de coeficientes do polinômio no Matlab.

Uma vez que fazemos isso vamos realizar a operação de divisão utilizando a função d e c o n v que é uma função própria para a operação de divisão de polinômios.

Passo 2

Agora que sabemos o passo a passo da resolução, vamos implementar as informações da questão no Matlab.

Primeiramente vamos implementar os vetores dos coeficientes dos polinômios D   e   Q para realizar a operação de divisão posteriormente.

D = [ 1         1 ]

Q = [ 1     - 3       0         2     - 3 ]

Na hora de implementar o vetor dos coeficientes do polinômio Q nós colocamos um elemento a mais que é o 0 .

Esse elemento surge pois no polinômio original não aparece o x 2 logo colocamos o elemento 0 no lugar que ele ocuparia.

Para a realização da divisão vamos utilizar a função deconv, onde a sua sintaxe é a seguinte:

q     r e s t o = d e c o n v ( n u m e r a d o r , d e n o m i n a d o r )

Onde a função d e c o n v gera duas saídas, o quociente e o resto da divisão.

E suas entradas precisam de dois argumentos, o primeiro argumento é obrigatoriamente o numerador que no nosso caso é o Q . Já o segundo argumento é o denominador que no nosso caso se torna o D.

Implementando tudo no Matlab temos:

Executando o código temos:

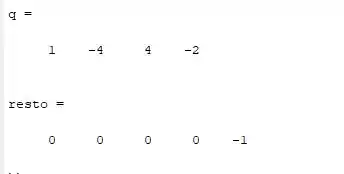
Resposta

O Resto da divisão de polinômios corresponde a um polinômio constante igual a -1.