Exercícios Resolvidos de Operações com Polinômios (Zeros, Soma, Produto e Divisão de Polinômios)
Ver TeoriaEnunciado
Uma esfera de alumínio é utilizada como boia sinalizadora. A esfera possui raio externo igual a 60cm e espessura da capa de alumínio de . A densidade do alumínio é . A bóia foi jogada ao mar, onde a densidade da água vale .
Elabore uma Rotina em Matlab que permita calcular a altura do nível do mar até o topo da bóia.
Dica: A partir de cálculos de equilíbrios de força é possível obter a seguinte equação que modela a física do processo:
Passo 1
A questão pede para calcularmos a posição de equilíbrio que a bóia estará acima do nível do mar. A equação que modela isso pode ser obtida através de cálculos de equilíbrios semelhantes a aqueles vistos nos cursos básicos de física, porém, como o foco aqui é programação, a equação final já foi fornecida para você.
Então uma vez que temos todos os dados para a resolução da questão, vamos elaborar um pequeno algoritmo para a resolução da mesma:
O algoritmo para a resolução desse exercício é dado por:
- Entrada de dados:
- Criação do vetor dos coeficientes da equação de segundo grau
- Implementação da função zeros para encontrar o valor de h que satisfaz a igualdade.
AHHH lembrar que o
Passo 2
Uma vez que criamos o algoritmo basta apenas inseri-lo no Matlab, sendo assim:
Primeiramente vamos colocar a entrada de dados:
Agora que implementamos a entrada de dados vamos criar o vetor com os coeficientes da equação cúbica:
Agora basta implementar a função roots para o cálculo dos valores de h que satisfazem a equação cúbica:
Seu codigozinho deve estar mais ou menos assim:
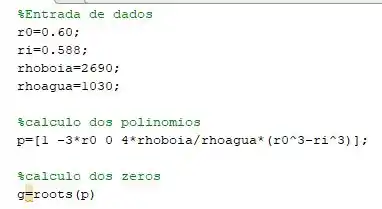
Executando o código na sua janela de command window deve mostrar a seguinte resposta:
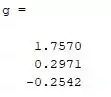
Analisando as respostas vemos que tanto a última quanto a primeira raiz não tem sentido físico, a última nos remete a um raio negativo, algo fisicamente sem sentido.
Já a primeira raiz nos dá um valor de raio maior que o raio do próprio cilindro, o que também não tem um sentido físico.
Então só resta que o valor de h seja aproximadamente 0.2971 cm.