Exercícios Resolvidos de Operações com Polinômios (Zeros, Soma, Produto e Divisão de Polinômios)
Ver TeoriaEnunciado
Um tanque de gás possui o formato de um cilindro com extremidades hemisféricas.
O raio do cilindro é e o comprimento é . Determine considerando que o volume do tanque é
Passo 1
A questão fala de um reservatório onde as extremidades são calotas esféricas e o corpo é um cilindro, ou seja, é formado por um cilindro e duas semi-esferas. Sendo assim o volume total do reservatório é dado por:
A questão também nos dá uma informação importante que o Raio do cilindro é de e o comprimento do cilindro de de
Então a fórmula para o cálculo do volume se torna:
Sendo assim a equação final fica;
Então a questão pede para utilizar essa equação final e encontrar um valor de fisicamente válido, para isso vamos utilizar da função para encontrar um valor de para que a equação cúbica acima seja nula.
Passo 2
Dado que temos que a equação cúbica se torna:
Logo o vetor dos coeficientes da equação cúbica se torna (não esqueça dos coeficientes nulos do e do )
Agora iremos implementar a função roots:
Passo 3
Se colocou tudo certinho seu programa no Matlab deve estar algo mais ou menos assim:
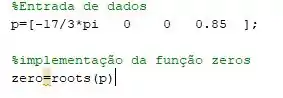
Executando esse mini código na sua janela de command Window deve mostrar algo assim:
De todas as possíveis respostas a única que é fisicamente aceitável é a resposta de
Pois as demais respostas estão no domínio dos complexos o que não gera uma resposta fisicamente significativa.