Calcule as seguintes expressões abaixo:
- Calcule a divergência de z
- A matriz A é dada por e calcule a matriz inversa de
- Dado o vetor calcule o cosseno desse vetor.
Passo 1
Para calcular a divergência do vetor, precisamos primeiramente inseri-lo de forma simbólica.
Isso torna-se necessário porque estamos com variáveis que não tem um valor numérico definido, então a única forma de calcular essas operações no Matlab é via variável simbólica. Operações realizadas em função de algo que não apresente um valor numérico exige que indiquemos no Matlab que as variáveis são simbólicas.
Pensa comigo, se eu não digo quais são as variáveis de entrada, qual é a entrada de dados? Ou seja, o primeiro bloco da programação é nulo, vou realizar uma operação em algo que eu não defini, por isso utiliza-se variável simbólica nessa alternativa.
E relembrando uma coisa que já foi vista em outros tópicos: quando se define uma variável simbólica, isso está além de se a natureza é vetorial ou escalar, ou seja, a variável simbólica serve tanto para funções escalares quanto para funções vetoriais.
Após isso utiliza a função divergência para calcular o divergente do vetor.

Aqui o Matlab separou os elementos do vetor Z por uma vírgula, isso é algum elemento da sua própria configuração que porventura desconheço o motivo, pois podemos separar os elementos de uma linha de duas formas a primeira é o que utilizamos que é espaçamento simples a outra é colocar uma vírgula.
Por algum motivo meu Matlab está configurando assim, mas tanto um quanto o outro está correto.
Mas o que importa é que na workspace ele está entendendo que estou criando um vetor linha como mostrado abaixo:

Passo 2
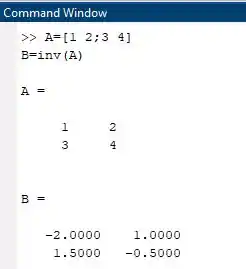
Para resolver essa questão primeiramente precisamos inserir a matriz e após isso utilizamos a função inversa vista na tabela da aula, logo precisamos implementar a matriz dentro do Matlab.
Primeiramente vamos inserir a primeira linha onde precisamos espaçar os elementos apenas com um espaçamento simples.
A
Para implementar a segunda linha precisamos dar um “;” para indicar que vamos implementar a segunda linha e vamos separar cada elemento da segunda linha por um espaçamento simples, resultando a seguinte matriz:
A
Passo 3
E ae galera vamos resolver esse problema? Para isso primeiramente vamos inserir k vetor ok?
Uma vez que o vetor está inserido, vamos apenas calcular o cosseno desse vetor, ou seja, vamos calcular o cosseno de cada elemento dentro do vetor.
Para isso precisamos apenas chamar a função cosseno e no seu argumento de entrada inserir o vetor que desejamos calcular o cosseno.
Sendo assim, a sintaxe se torna:
Onde a variável Y está nos mostrando o cosseno de cada elemento do vetor V.

Resposta
Ei, a resposta está no passo a passo :)