Dada a matriz:
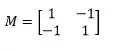
A operação é igual a:
Passo 1
Essa questão é uma questão bem típica da álgebra linear que existe uma demanda de cálculos consideravelmente grande.
Para a resolução analítica da questão devemos lembrar das operações de multiplicação de matrizes, que equivale por exemplo a:
Agora imagina só, você realiza essas operações até resolver aqueles polinômios da questão?
Trabalhoso demais né?
Ai que vem a vantagem de resolver isso no Matlab, iremos precisar apenas de duas linhas.
A primeira vamos inserir a matriz e na segunda linha vamos inserir o polinômio, pois, quando eu indico no Matlab a operação ele automaticamente já entende que tou fazendo
E isso funciona com as demais potências.
Passo 2
Agora que já discutimos a questão no passo 1, vamos inserir a matriz dentro do Matlab.
Para isso vamos precisar lembrar da sintaxe, para inserirmos os elementos da primeira linha precisamos apenas separar os elementos por espaços simples dentro de uma chave.
Logo a primeira linha da matriz fica:
Agora precisamos inserir a segunda linha basta colocar o ponto e vírgula, isso indica ao Matlab que vamos começar a escrever a segunda linha da matriz, logo:
Uma vez que inserirmos a matriz no Matlab, vamos agora implementar o polinômio da questão em si da seguinte forma:
Passo 3
Inserindo tudo na janela de command Windows deve mostrar algo mais ou menos assim para você:
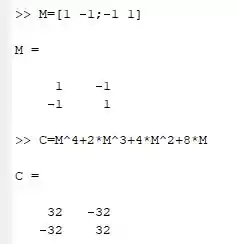
Resposta
Ei, a resposta está no passo a passo :)