Dado o sistema de equações:
Encontre os valores de pertencente aos reais, pelo o qual o sistema de equações possui uma solução única e real.
Passo 1
A questão é uma aplicação de resolução de sistema de equações lineares, tem diversas formas de fazer ela.
Porém, dessa vez iremos resolver pelo método da matriz inversa. Pois, como geralmente é mostrado no ensino médio seja um sistema de equações na forma matricial.
Se pudermos escrever o sistema da seguinte forma:
Nós temos que a solução é
Então, para resolver essa questão precisamos explicitar todas as soluções em função de
E assim julgar os valores de pelo o qual nosso sistema satisfaz as condições desejadas da questão.
Passo 2
Analisando o sistema de equação podemos notar que podemos decompor em três matrizes, que são as matrizes:
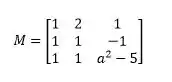
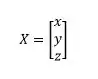

E podemos perceber que se realizarmos a seguinte operação matricial:
Iremos retornar para o sistema de equações originais.
Logo, para resolver o sistema de equações precisamos implementar primeiramente essas três matrizes no Matlab.
Então vamos lá.
Passo 3
Primeiramente precisamos notar que quando formos inserir essa matriz no Matlab existe uma variável simbólica dentro, isso mesmo é a variável .
Então vamos primeiramente defini-la como uma variável simbólica.
Agora vamos inserir as matrizes, se caso você inserir cada matriz certinho deve chegar em algo mais ou menos assim:

Uma vez que implementamos precisamos resolver o sistema de equação linear, para isso vamos usar a função inversa.
Basta escrever na sua Workspace a seguinte equação:
Ou seja, a solução é a inversa da matriz M multiplicado pela matriz B e chegaremos no seguinte conjunto de soluções:

Passo 4
Para finalizar vamos analisar as soluções, como podemos ver todas as soluções têm denominadores do tipo , onde as raízes são .
Ou seja, quando o valor de é igual a o denominador da , e como sabemos da matemática básica qualquer divisão por zero é uma indeterminação.
Ou seja, excerto qualquer outro valor de produz uma solução única e real.
Resposta
Ei, a resposta está no passo a passo :)