Dada as seguintes matrizes:
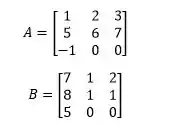
E uma suposta Matriz C que é dada pelo produto das Matrizes A e B, qual é o elemento da matriz C?
Passo 1
Opa galerinha, essa questão é uma questão bem típica de exercícios de geometria analítica.
A ideia aqui é executar a multiplicação entre as matrizes para poder identificar o elemento da matriz .
Não é uma tarefa muito difícil de fazer manualmente, porém, o Matlab está aí para facilitar nossas vidas, então vamos lá utilizá-lo.
Primeiramente precisamos implementar cada matriz no Matlab, após isso basta realizar o produto das matrizes A e B e rapidamente teremos a matriz C.
Mas como identificar o elemento ?
Basta usar o comando
Esse comando faz o seguinte, ele procura o elemento da intersecção entre a segunda linha e segunda coluna da Matriz C e o anexa na variável G que você mesmo definiu, respondendo assim a sua questão.
Passo 2
Agora que já discutimos a questão no passo 1, vamos inserir a matriz dentro do Matlab.
Para isso vamos precisar lembrar da sintaxe, para inserirmos os elementos da primeira linha precisamos apenas separar os elementos por espaços simples dentro de uma chave.
Logo a primeira linha da matriz fica:
Agora precisamos inserir a segunda linha basta colocar o ponto e vírgula, isso indica ao Matlab que vamos começar a escrever a segunda linha da matriz, logo:
Seguindo essa regrinha sucessivamente podemos escrever as Matrizes e da seguinte forma:
E consequentemente a Matriz C é dada por
E para descobrir o Elemento da matriz C que nos interessa basta escrevermos:
Que isso irá procurar na matriz C o elemento e anexá-lo na variável C imprimindo na janela de command windows
Passo 3
Inserindo tudo na janela de command Windows deve mostrar algo mais ou menos assim para você:

Resposta
Ei, a resposta está no passo a passo :)