Crie uma rotina para resolver o seguinte sistema de equações lineares com o Matlab:
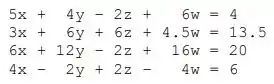
Dica : deixe o sistema na forma matricial e utilize a última tabela da aula de matrizes e operações
Passo 1
Primeiramente para resolver essa questão precisa reescrever o sistema de equações sob a forma matricial, sendo assim esse sistema na forma matricial se torna:
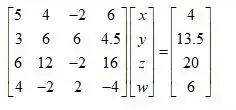
E vamos chamar a matriz de coeficientes de A e o vetor à direita da equação de b.

Para resolver esse sistema de equações lineares basta lembrar da função linsolve que está na tabelinha da aula.
Agora vamos programar!
Passo 2
O código no Matlab se torna algo mais ou menos assim. Primeiro vamos declarar 4 vetores e cada um deles corresponde a uma das linhas da matriz A. Para formar vetores, os elementos são separados por espaços.
V1 = [5 4 -2 6]
V2 = [3 6 6 4.5]
V3 = [6 12 -2 6]
V4 = [4 -2 2 -4]
Agora que temos suas linhas definidas, criamos a matriz A com os elementos (as linhas) listadas na ordem correta e separadas por ponto e vírgula.
A = [ V1 ; V2 ; V3 ; V4 ]
O vetor b é uma matriz coluna, então também terá seus elementos separados por ponto e vírgula.
B = [ 4 ; 13.5 ; 20 ; 6 ]
Agora usamos o comando linsolve pra resolver o sistema de equações. Nos argumentos entram a matriz de coeficientes A e o vetor de termos independentes b, nessa ordem.
X = linsolve (A,b)
Passo 3

Agora o Matlab irá montar a matriz e resolver com a função:

Resultando X=0,9433 y=1,8821 z=0,7415 w=-1,1270
Resposta
Ei, a resposta está no passo a passo :)