17. Faça o gráfico e encontre o conjunto imagem das funções abaixo. Identifique os pontos em que o gráfico intersecta os eixos coordenados e os pontos nos quais há uma mudança no comportamento do gráfico (por exemplo, um vértice de uma parábola).
c)
b) .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nessa questão, temos que obter o gráfico, o conjunto imagem, os pontos em que o gráfico intersecta os eixos coordenados e também os pontos onde o comportamento do gráfico muda.
Tem ideia de como fazer isso? 👀
Para obter o gráfico da função, vamos esboçar alguns pontos da função e ligá-los, esboçando seu gráfico.
Para obter o conjunto imagem, podemos imaginar que esse conjunto são os possíveis valores que a função pode assumir, ou seja, os possíveis valores para .
Para obter os pontos onde o gráfico pertence aos eixos, fazemos e na função.
E por fim, analisando os gráficos, podemos obter os pontos onde a função muda de comportamento.
Entendeu? Bora começar! 😎
Passo 2
Para a função , vamos começar plotando alguns pontos de seu gráfico.

Plotando esses pontos no plano cartesiano e estimando o comportamento do gráfico de , podemos esboçar a função.
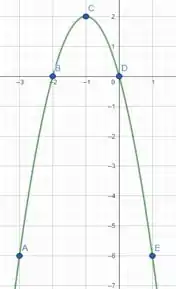
A partir do gráfico, podemos obter informações interessantes, por exemplo:
Os pontos e são os pontos que pertencem aos eixos coordenados.
O ponto é o vértice da função, antes dele, a função é crescente e depois a função é decrescente.
E por último, podemos ver que a imagem da função são os valores entre e já que fora desse intervalo a função não assume nenhum valor.
Tranquilo até aqui?
Passo 3
Agora fazemos o mesmo para a função

Plotando os pontos e estimando o comportamento da função...
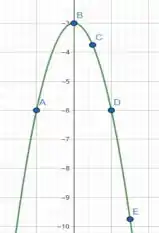
A partir do gráfico de , podemos ver que o ponto é o vértice de e também é o único ponto que pertence a um eixo coordenado.
E também, podemos ver que a imagem de é dada por
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
C) , e pertencem aos eixos coordenados e é o vértice da função.
D) , é o vértice e pertence ao eixo .