Um bloco de encontra-se em repouso e apoiado sobre um plano inclinado em em relação ao solo. Considerando a gravidade local igual a , determine o módulo da força que o plano inclinado exerce sobre o bloco.
Passo 1
Faaaala aí, tudo beleza? Vamos para mais uma questão sobre Plano Inclinado!
Vamos começar separando as informações importantes do enunciado!
Temos que:
Show, vamos montar nosso diagrama de forças para entender melhor a situação! Na situação descrita, vamos ter duas forças, o Peso que aponta para baixo e a força que o plano exerce sobre o bloco: a força normal (a que queremos calcular). Então, ficamos com:
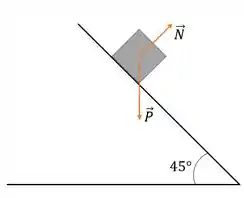
Passo 2
Show, agora que já entendemos melhor o que está acontecendo vamos partir para cima da questão na prática!
Queremos encontrar a normal, só que como o plano está inclinado! Então vamos definir os eixos e inclinados também
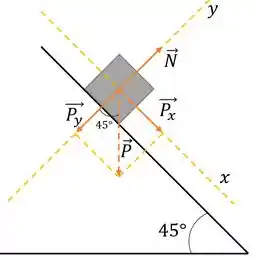
Perceba que a força Normal já ficou certinha no nosso eixo , mas a força Peso ficou meio inclinada com relação a esses eixos.
Então, podemos decompor a força Peso nas componentes e da forma que foi mostrada na figura acima.
Passo 3
Show, então podemos ver que no eixo , a força resultante é dada por
Como os vetores estão em sentidos opostos, vamos admitir o eixo positivo para “cima”. Então a força Normal será positiva e a componente do Peso no eixo será negativa.
Perceba que tiramos as setinhas de cima das letras, isso significa que estamos trabalhando com a intensidade de cada força (seus módulos)!
Como no eixo o bloco não está “afundando” no plano nem flutuando, então
Substituindo na formulinha alí de cima
Passando o para o outro lado
Passo 4
Show, o que a gente precisa agora é achar esse , como ele é uma componente de precisamos saber devemos multiplicar por seno ou por cosseno, vou te explicar como descobrir isso. Vamos focar na força Peso
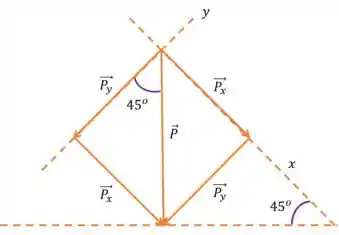
O ângulo da do plano inclinado sempre será igual aquele da força Peso com a sua componente em . Guardem essa informação no coração, vocês irão usar muito isso nas questões de plano inclinado.
Então, se pegarmos só os vetores que formam o triângulo , e
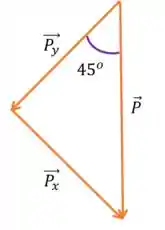
Podemos usar a trigonometria
Que no nosso caso será
Passando o para o outro lado multiplicando
O cosseno de vale e o peso é a massa vezes a gravidade, ambas informadas no enunciado. Então temos que:
Podemos cortar com ficando com
Que dá
É a opção e)
Resposta
e)