Um plano inclinado forma um ângulo de com a horizontal. Ao longo deste plano é lançado um bloco de massa com velocidade inicial , como indicado na figura. Qual a força de atrito em , que atua sobre o bloco para fazê-lo parar? (considere o coeficiente de atrito dinâmico igual a
Considere
Passo 1
Faaaala aí! Vamos pra cima de mais uma questão sobre plano inclinado!
Bom, a gente tem um desenho bonitinho que já diz muita coisa pra gente, vamos separar agora as informações do enunciado:
Com essas informações a gente já vai ter que
Então
Vamos fazer o diagrama de forças para entender melhor a situação
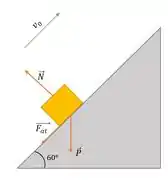
Perceba que a força de atrito ficou no sentido de descida do plano e não no de subida, como estamos acostumados. Isso porque a velocidade inicial do bloco está subindo a rampa, então o atrito tem que ter sentido oposto ao movimento.
Passo 2
Beleza, agora que entendemos o diagrama de forças, vamos começar separando a força peso em duas componentes, uma paralela ao plano e uma perpendicular ao plano.
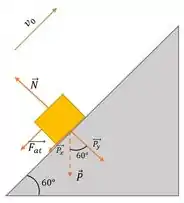
Como a força de atrito é dada pra gente por
Show, agora o que vamos fazer é achar o valor da normal, na perpendicular, temos que:
E a força resultante na perpendicular ao plano é desse jeitinho aqui:
Como cada força está apontando para um lado, definir que a Normal seja positiva, então a força tem que ser negativa
Perceba que estou escrevendo sem as setinhas em cima das letras. Fiz isso porque agora estamos trabalhando com as intensidades das forças e não mais com os vetores em si.
Como a força resultante tem que ser nula porque o bloco não afunda no plano e nem sai voando, então
Colocando essa informação na nossa fórmula da força resultante
Passando o para o outro lado, temos que:
Passo 3
Beleza, vamos lá calcular então.
Como é uma componente do peso que, no caso, está colada com o ângulo então vamos multiplicar o peso pelo cosseno
Vimos láá no passo que
Então temos que
Perfeitinho, temos então que
Passo 4
Beleza, achamos a normal, a força de atrito é:
Acabamos de achar a normal e (o coeficiente de atrito) é dado no enunciado, então temos que
Resposta
a)