Determine a aceleração, sabendo que e .
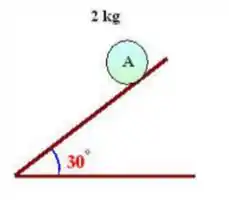
Passo 1
Faaaala galerinha, tudo certinho? Vamos pra mais uma questão sobre plano inclinado!
Bom, o enunciado dá pra gente algumas informações importantes, tanto na parte escrita quanto na imagem, vamos separá-las então!
E pede pra gente a aceleração
Vamos começar fazendo o diagrama de forças! Como o enunciado não fala nada sobre a força de atrito, vamos considerar que o nosso plano seja perfeitamente liso!
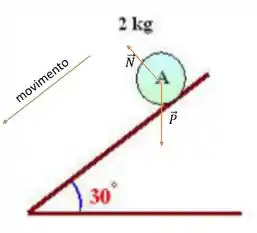
Show! Como o movimento é paralelo ao plano e a força Normal é perpendicular a ele, então a normal não afeta em nadica de nada para o movimento.
Maaaaas o peso afeta, vamos então decompor o peso em duas componentes, uma paralela ao movimento e uma perpendicular ao movimento, ficando com:
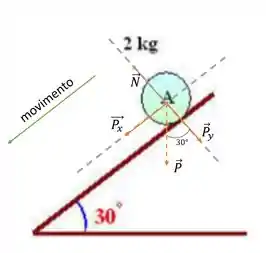
Perceba que coloquei um ângulo entre a força Peso e sua componente . Esse ângulo sempre será igual ao ângulo do plano inclinado com a horizontal! Anotem isso em algum lugar para não esquecer!
Passo 2
Show, agora que a gente já entendeu o que está acontecendo com a nossa bolinha, vamos passar para mão na massa!
Como na direção do movimento os vetores e estão perpendiculares ao movimento, não afetam na resultante desse nosso movimento, o único vetor que afeta essa nossa resultante do movimento é , então podemos dizer que
E pela segunda lei de Newton, temos que
Então podemos concluir que
Passo 3
Então vamos lá, quem é esse
Bom, é uma componente do peso, e como ela está sem encostar no ângulo de vamos usar o seno multiplicado pelo peso
O peso é ninguém mais ninguém menos que a massa vezes a gravidade, temos ambas informações no enunciado
Agora vamos colocar isso para achar , já que o seno é dado no enunciado
Passo 4
Agora vamos partir pra cima da segunda lei de Newton
Temos a massa e , então
Passando o dividindo, temos: