Um estudante de deseja medir seu peso ficando de pé sobre um skate que desce uma rampa, conforme a figura. Admita que não haja atrito, de modo que a força exercida pela rampa sobre o skate seja normal a rampa. Qual é a indicação da balança para ?

Admita
Passo 1
Faaala aí, vamos pra mais uma questão sobre Planos Inclinados!
Bom, esse doido aí quer saber quanto a balança mostra, e já vou te adiantar pra não se apressar e achar que o que a marca vai ser o peso dele, seria muito facinho né? Hehe mas vamos ver porquê disso!
Bom, vamos começar fazendo o diagrama de forças, como não temos atrito, ficamos com:
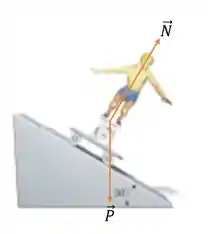
O que vamos fazer é decompor o peso em dois eixos:
- Paralelo ao plano inclinado (vamos chamar de
- Perpendicular ao plano inclinado (vamos chamar de
Fazendo isso ficamos com:
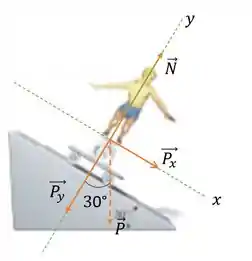
Passo 2
Show, como queremos achar a normal vamos olhar pro eixo !
No eixo a força resultante é zero, já que o menino não saiu voando e nem afundou o chão!
Então temos que
E, como temos dois vetores opostos, podemos dizer que
(considerando o referencial pra cima positivo)
Perceba que tirei as setinhas de cima das letrar. Fiz isso porque agora estamos trabalhando com as intensidades de cada força e não mais com os vetores, beleza?
Então temos que
Passando para o outro lado, temos
Passo 3
Para calcularmos , basta perceber que ele está colado com o ângulo, então ele vai ser o peso vezes o cosseno de
Então temos que
Para acharmos o peso, basta multiplicar a massa do menino pela gravidade, ou seja
E como
Ficamos com
Isso nos dá
Como , então
E como ,