Um corpo de massa igual a é abandonado sobre um plano inclinado cujo ângulo de elevação é de . O coeficiente de atrito entre o corpo e o plano é desprezível.
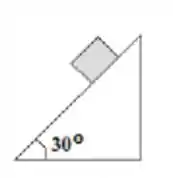
Admitindo-se . Determine:
- A aceleração do corpo ao descer o plano.
- A intensidade da reação normal de apoio
Passo 1
Faaaala aí, tudo certinho? Vamos continuar com nossos estudos sobre Plano Inclinado.
Vamos começar separando algumas informações importantes do enunciado, temos que
Com isso podemos encontrar o valor do peso:
Beleza, vamos guardar essa informação. Agora vamos fazer o diagrama das forças que atuam no bloco
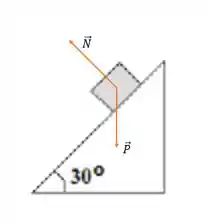
Já que o enunciado fala para desprezar o atrito, então ficaremos só com o Peso e a Normal mesmo.
Agora o que vamos fazer é decompor o peso em dois eixos:
- Paralelo ao plano inclinado (vamos chamar de
- Perpendicular ao plano inclinado (vamos chamar de
Fazendo isso ficamos com:
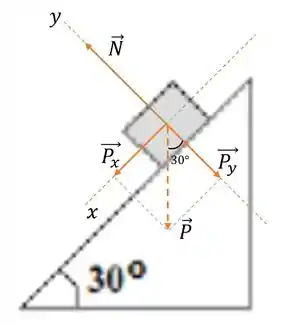
Perceba que coloquei um ângulo de alí em cima. Isso foi porque o ângulo que forma o plano inclinado com a horizontal se reflete entre a força peso e a sua componente ! Fiquem espertos com isso porque vai aparecer muitas vezes na vida de vocês ainda 😊
Passo 2
Vamos começar pela letra , que pede o valor da aceleração.
Esta letra está relacionada ao eixo , paralelo ao plano inclinado.
Como só temos um vetor nesse eixo, temos que:
Como está sem encostar no ângulo de , temos que ele é igual ao vetor vezes o seno
Sabemos que e o peso vale então
Então
E, de acordo com a 2ª lei de newton, temos que
Como a massa vale , temos que
Passando o dividindo, temos que
Passo 3
Show, agora vamos achar o valor da normal!
Temos que:
está colado com o ângulo de então ele é igual ao vetor vezes o cosseno
Como e o peso vale , temos que
E como só temos dois vetores no eixo , temos que
Então
Que vale aproximadamente