Determine a aceleração, sabendo que , , e
Passo 1
Faaaala aí gente bonita, tudo certinho? Vamos para mais uma questão sobre plano inclinado!
Bom, o enunciado dá para a gente algumas informações importantes, vamos separá-las bonitinho aqui:
E pede pra gente a aceleração:
Vamos começar fazendo o diagrama de forças! Como o enunciado não fala nada sobre a força de atrito, vamos considerar que o nosso plano seja perfeitamente liso!
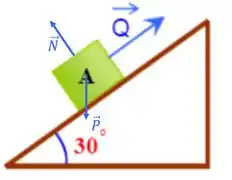
Show, na direção do movimento, a normal não afeta em nadica de nada, porque está na perpendicular, maaaaas o peso afeta, vamos então decompor o peso em duas componentes, uma paralela ao movimento e uma perpendicular ao movimento, ficando com:
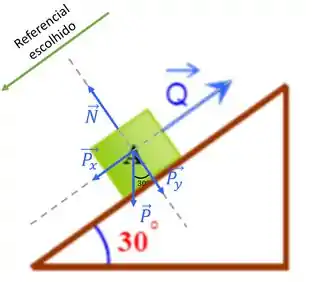
Como não podemos afirmar que o movimento tá indo pra cima ou pra baixo, vai depender das forças que atuam no sentido paralelo, vamos escolher arbitrariamente, se chutarmos certo, a aceleração vai ter sinal positivo; se chutarmos errado ela vai ter sinal negativo e vai ser na direção oposta ao que escolhemos. Mas não se preocupa que isso não vai mudar nosso resultado, belezinha? Vou escolher “pra baixo”, mas sendo paralelo ao plano 😊
Passo 2
Show, agora que a gente já entendeu o que está acontecendo com o nosso bloquinho, vamos passar para mão na massa!
Como na direção do movimento os vetores e estão perpendiculares ao movimento, não afetam na resultante desse nosso movimento, os vetores que afetam essa nossa resultante do movimento são e , então podemos dizer que
Como as forças e apontam em sentidos contrários, vamos definir que a força seja positiva, então será negativa
Perceba que tirei as setinhas de cima das letras. Isso porque agora estamos trabalhando com as intensidades dos vetores e não mais com os vetores em si.
E pela segunda lei de Newton, temos que
Então podemos concluir que:
Passo 3
Então vamos lá, quem é esse
Bom, é uma componente do peso, e como ela está sem encostar no ângulo de vamos usar o seno multiplicado pelo peso
O peso é ninguém mais ninguém menos que a massa vezes a gravidade, temos ambas informações no enunciado
Agora vamos colocar isso para achar , já que o seno é dado no enunciado
Passo 4
Agora vamos partir pra cima da segunda lei de Newton
As informações que temos são
Substituindo ficaremos com
Isso nos dá
Passando o dividindo, temos:
Opa, como a gente viu lá em cima não tem problema dar negativo, só que a aceleração vai estar para o outro lado do referencial! Como de costume, chutei errado, mas não tem problema não hehe ficamos com isso daqui então:
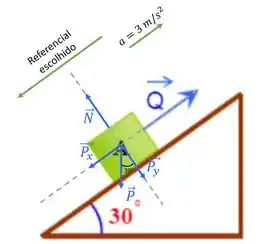
E o modulo da aceleração é: