O tubo em V simétrico na figura abaixo contém água estática e ar a . Qual é a pressão do ar na parte fechada no ponto ?
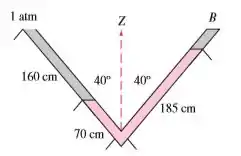
Passo 1
Uma questão de vasos comunicantes, porém agora temos um vaso inclinado.
Nada mudou, vamos continuar pegando dois pontos de mesma altura no mesmo fluido e falando que a pressão neles deve ser igual.
Os pontos escolhidos vão ser:
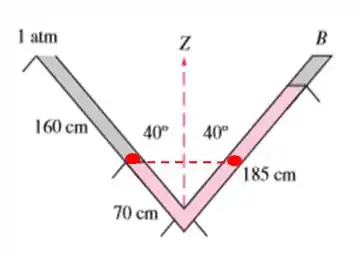
Já temos os pontos. O que muda nesse estilo de vaso é que não temos as alturas. Vamos ter que descobrir todas as alturas para podermos resolver o problema.
Lembre que na pressão o que importa é a distância vertical. Pois quando igualarmos as pressões vamos obter a equação do lado esquerdo:
E do lado do lado direito:
Então para resolvermos o problema temos que encontrar a altura , alturas essas que correspondem a:
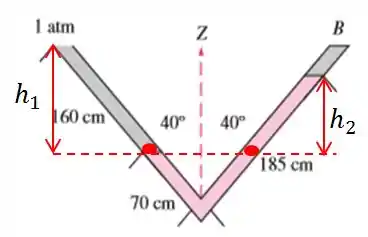
Para descobrir essas alturas, vamos ter que usar algumas relações trigonométricas.
Vamos usar o fato de que seno de um ângulo é igual a razão entre o lado oposto ao ângulo e a hipotenusa
Mas que ângulo é esse? Bem, a imagem nos forneceu que o ângulo entre um dos lados do vaso e a vertical é . Como a vertical faz com a horizontal, o vaso faz com a horizontal.
Então conseguimos descobrir a altura , assim:
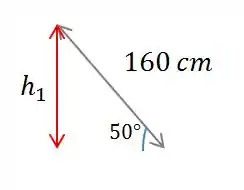
Usando a relação do seno, temos
Com o auxilio de uma calculadora temos:
Observação:
Então você também pode calcular como:
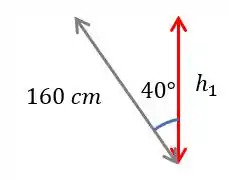
Agora só falta descobrir e para isso faremos o mesmo:
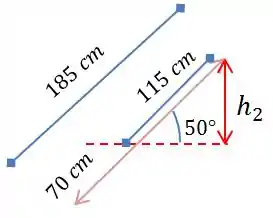
Utilizando da imagem dada pelo enunciado conseguimos descobrir o comprimento de água acima do ponto analisado, e tendo este valor descobrir a altura:
Passo 2
Agora que temos as alturas, faltam apenas as densidades. A da tem que lembrar que é e a do ar vamos ter que pesquisar em um livro ou na internet.
A massa especifica do ar é aproximadamente:
Assim, podemos resolver a questão. Igualando as duas equações mostradas lá em cima temos:
Lembre-se de usar as unidades correta, por isso transformamos e
Resolvendo a equação temos: