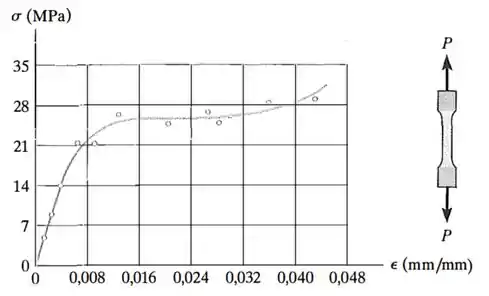
O diagrama tensão-deformação para o polietileno que é utilizado para revestir cabos coaxiais é determinado por um ensaio com um corpo de prova com comprimento de referência de . Se uma carga aplicada ao corpo de prova desenvolver uma deformação , determine o valor aproximado do comprimento do corpo de prova medido entre os pontos de referência quando a carga é removida. Considere que o corpo de prova se recupere elasticamente.
Passo 1
O que está acontecendo?
O corpo de prova tem um comprimento inicial e foi carregado até atingir uma deformação , o que corresponde a uma tensão :
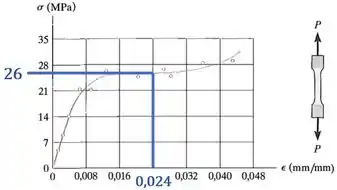
Ok!
Agora vamos pensar...
A deformação total no corpo é igual à soma das deformações elástica (reversível) e plástica (irreversível) que foram sofridas pelo corpo:
Dessa forma, quando o corpo é descarregado, ele vai recuperar a deformação elástica e a deformação final nele vai ser igual à deformação plástica (que não é recuperada):
E, como a recuperação da deformação elástica sempre segue a Lei de Hooke, temos que:
Sendo assim, a deformação final no corpo vai ser:
Onde é a deformação de e é a tensão de que foram atingidas pelo corpo.
E o que é que o exercício quer?
Ele quer saber qual é o comprimento final do corpo de prova depois que carga é removida.
Esse comprimento final vai ser igual ao comprimento inicial do corpo mais a variação de comprimento sofrida:
E a variação de comprimento vai ser igual ao comprimento inicial multiplicado pela deformação final , de tal forma que:
Então como vamos resolver o exercício?
Primeiro, vamos ter que encontrar o módulo de elasticidade do material do corpo de prova.
Feito isso, vamos poder encontrar a deformação final no corpo , e, em seguida, encontrar o comprimento final .
Passo 2
Começando pela determinação do módulo de elasticidade do material do corpo de prova!
Da Lei de Hooke , temos que:
Sendo assim, podemos escolher um ponto da região do Diagrama Tensão-Deformação do material que segue a Lei de Hooke:
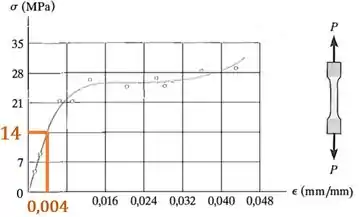
E utilizar os valores de e nesse ponto para calcular :
Passo 3
Agora que sabemos o módulo de elasticidade do material, já podemos calcular a deformação final :
Substituindo a deformação atingida , a tensão atingida e o módulo de elasticidade , temos:
Calculando isso, encontramos que:
Passo 4
Por fim, podemos calcular o comprimento final do corpo de prova:
Substituindo os valores e , isso fica assim:
O que dá: